Combining the nodes

Table 1: The forward messages or expectations that are provided by the output of different types of nodes. The numbers in parentheses refer to defining equations. The multiplication and nonlinearity cannot provide the expected exponential.

Node type	$\left< \cdot \right>$	$\mathrm{Var}\left\{\cdot\right\}$	$\left< \exp\cdot \right>$
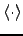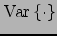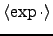Gaussian node	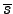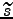$\overline{s}$	$\widetilde{s}$	(12)
Addition node	(20)	(21)	(22)
Multiplication node	(23)	(24)	-
Nonlinearity	(30)	(30),(31)	-
Constant	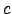$c$	0	$\exp c$

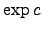Table 2: The backward messages or the gradients of the cost function w.r.t. certain expectations. The numbers in parentheses refer to defining equations. The gradients of the Gaussian node are derived from Eq. (10). The Gaussian node requires the corresponding expectations from its inputs, that is, 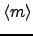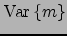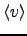$\left < m \right >$, $\mathrm{Var}\left\{m\right\}$, $\left < v \right >$, and $\left< \exp v \right>$. 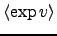Addition and multiplication nodes require the same type of input expectations that they are required to provide as output. Communication of a nonlinearity with its Gaussian parent node is described in Appendix C.

Input type	$\frac{\partial{\cal C}}{\partial\left< \cdot \right>}$	$\frac{\partial{\cal C}}{\partial\mathrm{Var}\left\{\cdot\right\}}$	$\frac{\partial{\cal C}}{\partial\left< \exp \cdot \right>}$
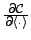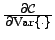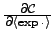Mean of a Gaussian node	(13)	(14)	0
Variance of a Gaussian node	(15)	0	(16)
Addendum	(25)	(26)	(27)
Factor	(28)	(29)	0

The expectations provided by the outputs and required by the inputs of the different nodes are summarised in Tables 1 and 2, respectively. One can see that the variance input of a Gaussian node requires the expected exponential of the incoming signal. However, it cannot be computed for the nonlinear and multiplication nodes. Hence all the nodes cannot be combined freely.

When connecting the nodes, the following restrictions must be taken into account:

1. In general, the network has to be a directed acyclic graph (DAG). The delay nodes are an exception because the past values of any node can be the parents of any other nodes. This violation is not a real one in the sense that if the structure were unfolded in time, the resulting network would again be a DAG.
2. The nonlinearity must always be placed immediately after a Gaussian node. This is because the output expectations, Equations (30) and (31), can be computed only for Gaussian inputs. The nonlinearity also breaks the general form of the likelihood (17). This is handled by using special update rules for the Gaussian followed by a nonlinearity (Appendix C).
3. The outputs of multiplication and nonlinear nodes cannot be used as variance inputs for the Gaussian node. This is because the expected exponential cannot be evaluated for them. These restrictions are evident from Tables 1 and 2.
4. There should be only one computational path from a latent variable to a variable. Otherwise, the independency assumptions used in Equations (10) and (21)-(24) are violated and variational Bayesian learning becomes more complicated (recall Figure 1).

Note that the network may contain loops, that is, the underlying undirected network can be cyclic. Note also that the second, third, and fourth restrictions can be circumvented by inserting mediating Gaussian nodes. A mediating Gaussian node that is used as the variance input of another variable, is called the variance source and it is discussed in the following.