


Next: Updating the posterior distribution
Up: Gaussian node
Previous: Gaussian node
Cost function
Recall now that we are approximating the joint posterior pdf
of the random variables 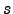 ,
, 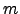 , and
, and 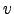 in a maximally
factorial manner. It then decouples into the product of
the individual distributions:
in a maximally
factorial manner. It then decouples into the product of
the individual distributions:
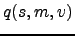 =
=
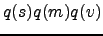 . Hence
. Hence 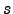 ,
, 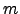 ,
and
,
and 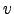 are assumed to be statistically independent a posteriori.
The posterior approximation
are assumed to be statistically independent a posteriori.
The posterior approximation 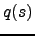 of the Gaussian variable
of the Gaussian variable 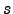 is defined to be Gaussian with mean
is defined to be Gaussian with mean
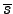 and variance
and variance
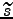 :
: 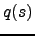 =
=
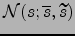 .
Utilising
these, the part
.
Utilising
these, the part
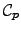 of the Kullback-Leibler cost function arising from
the data, defined in Eq. (7), can be computed in closed form.
For the Gaussian node of Figure 2, the cost becomes
of the Kullback-Leibler cost function arising from
the data, defined in Eq. (7), can be computed in closed form.
For the Gaussian node of Figure 2, the cost becomes
The derivation is presented in Appendix B of Valpola02NC
using slightly different notation. For the observed variables, this is the
only term arising from them to the cost function
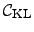 .
.
However, latent variables contribute to the cost function
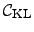 also
with the part
also
with the part
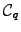 defined in Eq. (6), resulting from
the expectation
defined in Eq. (6), resulting from
the expectation
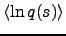 . This term is
. This term is
![$\displaystyle {\cal C}_{s,q} = \int_s q(s) \ln q(s)ds = -\frac{1}{2} [ \ln (2\pi\widetilde{s}) + 1]$](img87.png) |
(11) |
which is the negative entropy of Gaussian variable with variance
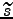 . The parameters defining the approximation
. The parameters defining the approximation 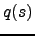 of the posterior distribution of
of the posterior distribution of 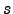 , namely its mean
, namely its mean
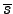 and
variance
and
variance
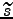 , are to be optimised during learning.
, are to be optimised during learning.
The output of a latent Gaussian node trivially provides the mean
and the variance:
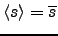 and
and
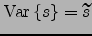 . The
expected exponential can be easily shown to be
Lappal-Miskin00,Valpola02NC
. The
expected exponential can be easily shown to be
Lappal-Miskin00,Valpola02NC
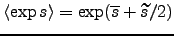 |
(12) |
The outputs of the nodes corresponding to the observations are known scalar
values instead of distributions. Therefore for these nodes
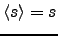 ,
,
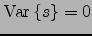 , and
, and
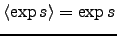 . An important conclusion
of the considerations presented this far is that the cost function of a
Gaussian node can be computed analytically in a closed form. This requires
that the posterior approximation is Gaussian and
that the mean
. An important conclusion
of the considerations presented this far is that the cost function of a
Gaussian node can be computed analytically in a closed form. This requires
that the posterior approximation is Gaussian and
that the mean
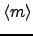 and the variance
and the variance
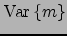 of the mean input
of the mean input 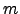 as well as the mean
as well as the mean
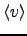 and the expected exponential
and the expected exponential
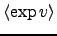 of the variance input
of the variance input 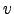 can be computed. To summarise, we have
shown that Gaussian nodes can be connected together and their costs
can be evaluated analytically.
can be computed. To summarise, we have
shown that Gaussian nodes can be connected together and their costs
can be evaluated analytically.
We will later on use derivatives of the cost function with respect
to some expectations of its mean and variance parents 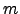 and
and 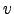 as
messages from children to parents. They are derived directly from
Eq. (10), taking the form
as
messages from children to parents. They are derived directly from
Eq. (10), taking the form



Next: Updating the posterior distribution
Up: Gaussian node
Previous: Gaussian node
Tapani Raiko
2006-08-28
![$\displaystyle = \frac{1}{2}\Big\{ \left< \exp v \right> \Big[\left(\overline{s}...
...{Var}\left\{m\right\} + \widetilde{s} \Big] - \left< v \right> + \ln 2\pi\Big\}$](img84.png)
![]() also
with the part
also
with the part
![]() defined in Eq. (6), resulting from
the expectation
defined in Eq. (6), resulting from
the expectation
![]() . This term is
. This term is
![]() and
and
![]() . The
expected exponential can be easily shown to be
Lappal-Miskin00,Valpola02NC
. The
expected exponential can be easily shown to be
Lappal-Miskin00,Valpola02NC
![]() and
and ![]() as
messages from children to parents. They are derived directly from
Eq. (10), taking the form
as
messages from children to parents. They are derived directly from
Eq. (10), taking the form