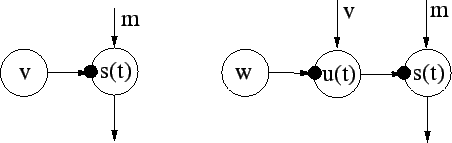 |
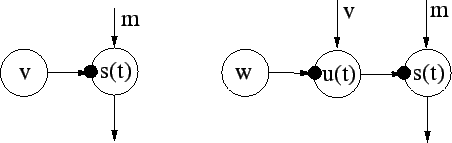 |
 |
In most currently used models, only the means of Gaussian nodes have
hierarchical or dynamical models. In many real-world situations the
variance is not a constant either but it is more difficult to model
it. For modelling the variance, too, we use the variance source
Valpola04SigProc depicted schematically in
Figure 3. Variance source is a regular Gaussian node
whose output ![]() is used as the input variance of another Gaussian node.
Variance source can convert prediction of the mean into
prediction of the variance, allowing to build hierarchical or
dynamical models for the variance.
is used as the input variance of another Gaussian node.
Variance source can convert prediction of the mean into
prediction of the variance, allowing to build hierarchical or
dynamical models for the variance.
The output ![]() of a Gaussian
node to which the variance source is attached (see the right subfigure
of Fig. 3) has in general a super-Gaussian
distribution. Such a distribution is typically characterised by long
tails and a high peak, and it is formally defined as having a positive
value of kurtosis (see ICABook01 for a detailed
discussion). This property has been proved for example in
Parra00NIPS, where it is shown that a nonstationary variance
(amplitude) always increases the kurtosis.
The output signal
of a Gaussian
node to which the variance source is attached (see the right subfigure
of Fig. 3) has in general a super-Gaussian
distribution. Such a distribution is typically characterised by long
tails and a high peak, and it is formally defined as having a positive
value of kurtosis (see ICABook01 for a detailed
discussion). This property has been proved for example in
Parra00NIPS, where it is shown that a nonstationary variance
(amplitude) always increases the kurtosis.
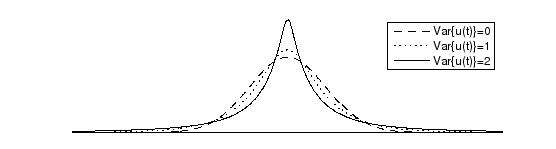
The output signal ![]() of the stationary Gaussian variance source depicted in
the left subfigure of Fig. 3 is naturally Gaussian
distributed with zero kurtosis. The variance source is useful in modelling
natural signals such as speech and images which are typically
super-Gaussian, and also in modelling outliers in the observations.
of the stationary Gaussian variance source depicted in
the left subfigure of Fig. 3 is naturally Gaussian
distributed with zero kurtosis. The variance source is useful in modelling
natural signals such as speech and images which are typically
super-Gaussian, and also in modelling outliers in the observations.