


Next: A hierarchical variance model
Up: Combining the nodes
Previous: Nonstationary variance
Linear independent factor analysis
In many instances there exist several nodes which have quite similar role
in the chosen structure. Assuming that
 th such node corresponds to
a scalar variable
th such node corresponds to
a scalar variable  , it is convenient to use the vector
, it is convenient to use the vector  =
=
 to jointly denote all the corresponding scalar variables
to jointly denote all the corresponding scalar variables
 . This notation is used in
Figures 5 and 6 later on. Hence we represent the scalar
source nodes corresponding to the variables
. This notation is used in
Figures 5 and 6 later on. Hence we represent the scalar
source nodes corresponding to the variables 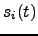 using the source vector
using the source vector
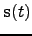 , and the scalar nodes corresponding to the observations
, and the scalar nodes corresponding to the observations
 using the observation vector
using the observation vector
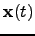 .
.
The addition and multiplication nodes can be used for building an
affine transformation
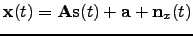 |
(32) |
from the Gaussian source nodes
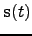 to the Gaussian observation nodes
to the Gaussian observation nodes
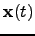 . The vector
. The vector
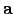 denotes the bias and vector
denotes the bias and vector
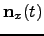 denotes the zero-mean Gaussian noise in the Gaussian node
denotes the zero-mean Gaussian noise in the Gaussian node
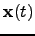 .
This model corresponds to standard linear factor analysis (FA) assuming
that the sources
.
This model corresponds to standard linear factor analysis (FA) assuming
that the sources 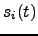 are mutually uncorrelated; see for
example ICABook01.
are mutually uncorrelated; see for
example ICABook01.
If instead of Gaussianity it is assumed that each source 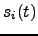 has
some non-Gaussian prior, the model (32) describes linear
independent factor analysis (IFA). Linear IFA was introduced
by Attias99, who used variational Bayesian
learning for estimating the model except for some parts which he
estimated using the expectation-maximisation (EM) algorithm. Attias used a
mixture-of-Gaussians source model, but another option is to use the
variance source to achieve a super-Gaussian source model.
Figure 5 depicts the model structures for linear factor
analysis and independent factor analysis.
has
some non-Gaussian prior, the model (32) describes linear
independent factor analysis (IFA). Linear IFA was introduced
by Attias99, who used variational Bayesian
learning for estimating the model except for some parts which he
estimated using the expectation-maximisation (EM) algorithm. Attias used a
mixture-of-Gaussians source model, but another option is to use the
variance source to achieve a super-Gaussian source model.
Figure 5 depicts the model structures for linear factor
analysis and independent factor analysis.
Figure 5:
Model structures for linear factor analysis (FA) (left) and
independent factor analysis (IFA) (right).
 |



Next: A hierarchical variance model
Up: Combining the nodes
Previous: Nonstationary variance
Tapani Raiko
2006-08-28
![]() has
some non-Gaussian prior, the model (32) describes linear
independent factor analysis (IFA). Linear IFA was introduced
by Attias99, who used variational Bayesian
learning for estimating the model except for some parts which he
estimated using the expectation-maximisation (EM) algorithm. Attias used a
mixture-of-Gaussians source model, but another option is to use the
variance source to achieve a super-Gaussian source model.
Figure 5 depicts the model structures for linear factor
analysis and independent factor analysis.
has
some non-Gaussian prior, the model (32) describes linear
independent factor analysis (IFA). Linear IFA was introduced
by Attias99, who used variational Bayesian
learning for estimating the model except for some parts which he
estimated using the expectation-maximisation (EM) algorithm. Attias used a
mixture-of-Gaussians source model, but another option is to use the
variance source to achieve a super-Gaussian source model.
Figure 5 depicts the model structures for linear factor
analysis and independent factor analysis.
