


Next: Example where point estimates
Up: Building Blocks for Variational
Previous: Form of the cost
Updating 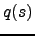 for the Gaussian node followed by a nonlinearity
for the Gaussian node followed by a nonlinearity
A Gaussian variable has its own terms in the cost function and it
affects the cost function of its children. In case there is a
nonlinearity attached to it, only the latter is changed. The cost
function of the children can be written in the form
![$\displaystyle {\cal C}_{\operatorname{ch}(s),p} = M \left< f(s) \right> + V [(\...
...ht>- \left< f(s) \right>_{\text{current}})^2 + \mathrm{Var}\left\{f(s)\right\}]$](img383.png) |
(64) |
where
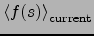 stands for the expectation using
the current posterior estimate
stands for the expectation using
the current posterior estimate 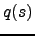 , and
, and 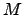 and
and 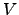 are constants.
are constants.
The posterior
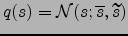 is updated to minimise the
cost function. For
is updated to minimise the
cost function. For
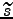 we get a fixed point iteration for the
update candidate:
we get a fixed point iteration for the
update candidate:
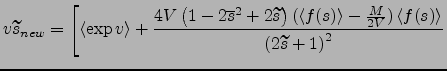 |
|
![$\displaystyle \left. - \frac{4 V \left(1- 4\overline{s}^2 + 4\widetilde{s}\right) \left< [f(s)]^2 \right>}{\left(4\widetilde{s} + 1\right)^{2}} \right]^{-1}$](img387.png) |
(65) |
And for
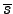 we have an approximated Newton's iteration update candidate
we have an approximated Newton's iteration update candidate
These candidates guarantee a direction, in which the cost function
decreases locally. As long as the cost function is about to increase
in value, the step size is halved. This guarantees the convergence to a
stable point.



Next: Example where point estimates
Up: Building Blocks for Variational
Previous: Form of the cost
Tapani Raiko
2006-08-28
![]() is updated to minimise the
cost function. For
is updated to minimise the
cost function. For
![]() we get a fixed point iteration for the
update candidate:
we get a fixed point iteration for the
update candidate: