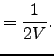Next: Addition and multiplication nodes
Up: Gaussian node
Previous: Cost function
The posterior distribution 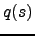 of a latent Gaussian node can be
updated as follows.
of a latent Gaussian node can be
updated as follows.
- The distribution
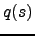 affects the terms of the cost function
affects the terms of the cost function
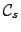 arising from the variable
arising from the variable 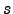 itself, namely
itself, namely
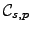 and
and
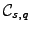 , as well as the
, as well as the
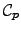 terms of the children of
terms of the children of 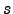 ,
denoted by
,
denoted by
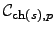 . The gradients of the cost
. The gradients of the cost
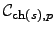 with respect to
with respect to
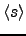 ,
,
 , and
, and
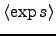 are computed according to Equations (13-16).
are computed according to Equations (13-16).
- The terms in
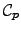 which depend on
which depend on
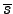 and
and
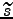 can be shown (see Appendix B.2) to be of the form
3
can be shown (see Appendix B.2) to be of the form
3
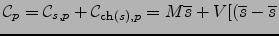 current current![$\displaystyle )^2 + \widetilde{s}] + E \left< \exp s \right>,$](img111.png) |
(17) |
where
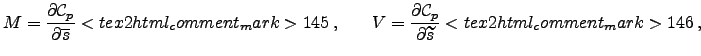 and and 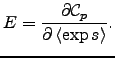 |
(18) |
- The minimum of
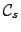 =
=
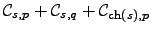 is solved.
This can be done analytically if
is solved.
This can be done analytically if 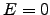 , corresponding to the case of
so-called free-form solution (see Lappal-Miskin00 for details):
, corresponding to the case of
so-called free-form solution (see Lappal-Miskin00 for details):
Otherwise the minimum is
obtained iteratively. Iterative minimisation can be carried out efficiently
using Newton's method for the posterior mean
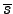 and a fixed-point
iteration for the posterior variance
and a fixed-point
iteration for the posterior variance
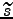 . The minimisation
procedure is discussed in more detail in Appendix A.
. The minimisation
procedure is discussed in more detail in Appendix A.



Next: Addition and multiplication nodes
Up: Gaussian node
Previous: Cost function
Tapani Raiko
2006-08-28
![]() of a latent Gaussian node can be
updated as follows.
of a latent Gaussian node can be
updated as follows.
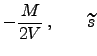 opt
opt