We shall start the derivation of the competition mechanism by considering a
network with only one neuron. We shall adopt the reconstruction error
minimisation approach, and start by defining the reconstruction
mapping (the mapping 
in section 2.1), which
has parameters 
:
The mapping is linear since the reconstruction is linearly dependent
on the parameters and the output y. Without any loss of
generality we can assume that the weight vector is
normalised to unity: 
. In order to obtain a
similar coding as in figure 3.1 B, we shall also require
the output y to be non-negative. By assuming a quadratic
reconstruction error and solving equation 2.1
(derivation is given in appendix A) we obtain
We have thus derived a neuron, which is most active when the direction of the input vector is the same as the direction of the weight vector.
Now suppose we have two neurons with reconstruction mapping
Again we can assume that the weight vectors 
are
normalised to unity and that the outputs 
are non-negative. We
expect the neurons to compete for the output. All competition should
be inhibitory, and therefore we shall require the outputs to be at
most what they would be if the neurons were be alone, that is, 
. This time the solution to
equation 2.1 turns out to be (derivation is given in
appendix A)
where 
and 
.
We have assumed that the degenerate case 
,
where c = 1, can be omitted. The solution for 
is similar with
indices 1 and 2 interchanged. The value 
is the projection of
the input on the weight vector . The value c gives a
measure for the similarity of the weight vectors. If c = 1, the
weight vectors are exactly the same. The smaller the c is the more
dissimilar are the weight vectors. We shall call the value c a
correlation, because in some cases
it can be interpreted as the measure
of correlation between 
and 
.
It is useful to define a new variable 
and examine its solutions:
We shall call the new variable a winning strength, because it
can be interpreted as the result of competition between the neurons.
Figure 3.2 shows the outputs and the winning
strengths 
as a function of the direction of input 
(equations 3.4 and 3.5). When only one
neuron is active, its winning strength is one. We can interpret this
so that the neuron has won the competition and is a full winner. When
both neurons participate in the representation of the input, the
winning strengths take values between zero and one. Both neurons are
winners to some extent, but neither is a full winner. When a neuron
has a zero output, also its winning strength is zero, and we can say
that the neuron has completely lost the competition.
By examining the equation 3.4 we notice that if the
correlation c between neurons is negative or zero, the winning
strength is one whenever the projection of the input on the weight
vector is positive: 
. This means that neurons with
dissimilar weight vectors have no mutual competition. The closer
c comes to one, the smaller become the outputs of the neurons.
This means that neurons with similar weight vectors compete most.
Another notable property of the winning strengths is that they depend
only on the direction of the input, not the magnitude. If the input
vector is multiplied with a positive constant, the winning
strengths remain unchanged.
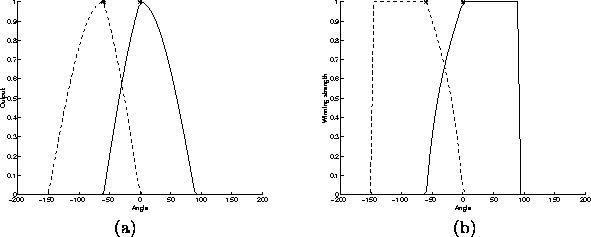
Figure 3.2:
The outputs (at the left) and the winning strengths
(at the right) of a network with two neurons are plotted as a
function of the angle of the input. The directions of the weight
vectors are denoted by `*'.
