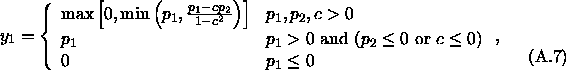
Next we prove that equation 3.4:
where 
and 
,
is the solution to the system of the following equations:
We assume here that the weight vectors 
are column vectors
with the same dimensionality as 
.
We know that the equations do not have a unique solution if the weight
vectors are identical. In that case the correlation between the
weight vectors would equal one. We assume that this degenerate case
can be omitted, and we always have 
.
The derivation is very similar to the previous one. At first we combine equations A.10, A.12 and A.13, which yields
We can further manipulate the norm appearing on the right hand side of
the equation. We denote the norm by 
.
Using the notations , 
and , and substituting
we can write
Let us denote the square matrix 
by S. We can now write
Note that because S is positive definite (we assumed ),
is a parabolic function.
We first find the solution without the constraints
A.14 and A.15. If 
is the
solution to the equation, then the gradient of at point
has to be a zero vector 
. The gradient of N is
and therefore the solution has to satisfy
The computation of 
yields
and thus the solution without the constraints is
Next we take into consideration the constraints
A.14 and A.15. If either of the 
is
less than or equal to zero, then 
= 0 and the solution to the
other output reduces to the case of one neuron, which has already been
solved. We can thus assume that both 
. The constraints
bound a rectangular area of allowed outputs. If the unconstrained
solution given by equation A.16 lies in that area, it is
also the solution to the constrained minimisation. Those cases, where
the unconstrained solution does not lie in the allowed area, are left
to examine. Due to the symmetry, the solutions to 
and 
are
identical except for the interchanged indices. We can therefore
consider only the solution to . Let us see what happens if 
. It is evident that the solutions to both of the outputs
in equation A.16 exceed the boundaries:
Because is parabolic, the best constrained solution lies
in the corner of the allowed area: 
and 
.
Now only those cases are left where 
, and c > 0. Let us
consider what happens if equation A.16 gives a solution
. We now that 
, and therefore 
. We see that
if the unconstrained solution to one of the outputs is under the
bound, then the other is over, and vice versa. Again the constrained
solution is found in the corner of the allowed area. This time one of
the outputs is zero and the other is . The solution to the case
can thus be formulated
Collecting together all the different cases yields the equation 3.4. This concludes the proof.
