In competitive learning, representational units compete for the right to represent the input [Rumelhart and Zipser, 1986]. It is unsupervised, which means that there is no need for any external teacher who is labelling the data or telling the learning system the desired outputs. The units, or neurons, which are used in the representation are called winners. Both reconstruction error minimisation and mutual predictability minimisation scheme can be interpreted as different methods for implementing the competition.
Hata et al. (1988) studied the visual cortex of cat and found inhibitory connections between neurons responsive to similar stimuli but not between neurons responsive to dissimilar stimuli. This means that neurons sensitive to similar features in the input compete with each other, while neurons sensitive to dissimilar features do not affect each other. This is probably the way in which the brain has implemented sparse coding, and we shall try to mimic this kind of competition behaviour. Our goal is to develop a computationally efficient algorithm which would implement the competition process. It is based on the following principles:
Figure 3.1 gives an example of how the competition could work. We have supposed that each neuron has a weight vector, which tells the direction of the input where the neuron is most sensitive. When the weight vectors span an orthogonal basis (figure A), the neurons respond to completely dissimilar inputs and there is no sense in finding winners. When there are more weight vectors, however, it is possible to choose a small subset of all neurons to represent the input. This produces more sharply tuned responses and a sparse code (figures B and C). The sharply tuned responses give more explicit information about the input, although the broadly tuned outputs contain the same information. If there are two sets of weight vectors which are tuned to different features of inputs, that is, the weights between sets are orthogonal, then the competition should occur only among neurons in one set. This way the sets could convey independent information and the system could process more information in parallel.
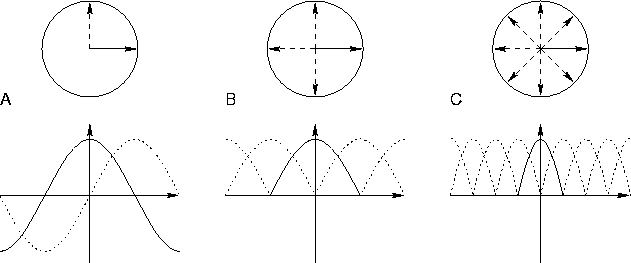
Figure 3.1:
The circles show the orientations of weight vectors of neurons.
Below the circles are the outputs of neurons for different
orientations of inputs. Orientation is on the x-axis and the
outputs of the neurons are on the y-axis. Figure A shows the
outputs of linear neurons. Two orthogonal neurons span the
2-dimensional input space. In figure B the outputs are limited to
be positive. Responses are more localised, and four neurons can
represent the 2-dimensional input space. The angles between
weight vectors are still at least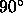 
, however, and there
is no competition. In figure C the neurons are no longer
orthogonal and they compete for the input. Competition between
similar neurons yields more sharply tuned responses and a sparse
code.