- ...kurtosis
- Kurtosis (K) is
the fourth-cumulant counterpart of variance. If variance is defined
as
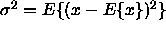, then 
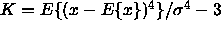is the normalised kurtosis. It
gives a measure of peakedness of a distribution. For Gaussian
distribution it is zero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...cortex
- Cortex is the surface of the brain. Cerebral cortex
is responsible for higher brain functions, e.g. sensory processing
and planning of motor commands.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...orthogonal
- For orthogonal matrix
W it holds
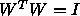. Orthogonal mapping is of form 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
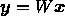- ...degenerate case
- If the input falls
equally far from two or more reconstruction vectors, then
equation 2.1 has degenerate solutions. If the input
has a continuous density, however, this happens with probability
zero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...algorithm
- Back-propagation is a popular
learning algorithm for MLP networks. See e.g. Haykin
(1994).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...correlation
- Correlation between
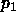and 
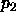is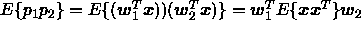 
. The value 
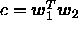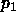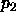equals the correlation between and , if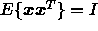 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fuzzy truth values
- In conventional logic propositions can be either true
or false. In fuzzy logic there can be propositions with
intermediate truth values. Value one means that the proposition is
absolutely true and value zero that it is absolutely false.
Intermediate values mean that the proposition is true and false to
some extent.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...neighbourhood
- The neurons are supposed to lie on a
low-dimensional map (cf. the 2-dimensional surface of the cortex).
The neighbourhood function
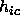is a measure of the cooperation
between neurons i and c. The cooperation is strongest for
neighbouring neurons and it decreases with the distance between
neurons. For more
information about SOM see the Master's Thesis of
Jaakko Hollmén.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.