Form of the Cost Function

The form of the part of the cost function that an output of a neuron affects is shown to be of the form $a \left< \cdot \right> + b [(\left< \cdot \right>- \left< \cdot \right>_{\text{current}})^2 + \mathrm{Var}\left\{\cdot\right\}] + c\left< \exp \cdot \right> + d$. If the output is connected directly to another variable, this can be seen directly from Equation (). When the output is connected to multiple variables, the sum of the affected costs is of the same form. Now one has to prove that the form stays the same when the signals are fed through addition and multiplication nodes.

If the cost function has the predefined form for s₁ + s₂, it has the same form for s₁, when regarding s₂ constant. This can be shown using () and ():

 

$$a\left< s_1+s_2 \right>+ b\left[\left(\left< s_1+s_2 \right>-\lef... ...s_2 \right>_{\text{current}}\right)^2+\mathrm{Var}\left\{s_1+s_2\right\}\right]$$ C =

$$+ c\left< \exp (s_1 + s_2) \right> + d$$ (4.37)

$$a\left< s_1 \right> + b\left[\left(\left< s_1 \right>-\left< s_1 \right>_{\text{current}}\right)^2+\mathrm{Var}\left\{s_1\right\}\right]$$ =

$$+ (c\left< \exp s_2 \right>)\left< \exp s_1 \right> + \left(d + a\left< s_2 \right> + b \mathrm{Var}\left\{s_2\right\}\right).$$

It can also be seen from () that when c=0 for the sum s₁ + s₂, it is zero for the addend s₁. This means that the outputs of product and nonlinear nodes can be fed through addition nodes.

If the cost function is of the predefined form with c=0 for the product s₁ s₂, it is similar for s₁, when regarding s₂constant. This can be shown using (, )

 

$$a\left< s_1s_2 \right>+ b\left[\left(\left< s_1s_2 \right>-\left<... ... \right>_{\text{current}}\right)^2+\mathrm{Var}\left\{s_1s_2\right\}\right] + d$$ C = (4.38)

$$\left(a\left< s_2 \right>+2b\mathrm{Var}\left\{s_2\right\}\left< s_1 \right>_{\text{current}}\right)\left< s_1 \right>$$ =

$$+ \left[b\left(\left< s_2 \right>^2+\mathrm{Var}\left\{s_2\right\... ...ft< s_1 \right>_{\text{current}}\right)^2+\mathrm{Var}\left\{s_1\right\}\right]$$

$$+ \left(d-b\mathrm{Var}\left\{s_2\right\}\left< s_1 \right>_{\text{current}}^2\right).$$

When one calculates the partial derivatives of a cost of this form

$$C_p = a \overline{s} + b [(\overline{s}-\overline{s}_{\text{current}})^2 + \widetilde{s}] + c\left< \exp s \right> + d,$$ (4.39)

one finds out that they are simply

$$\frac{\partial C_p }{ \partial \overline{s}}$$ = a (4.40)

$$\frac{\partial C_p }{ \partial \widetilde{s}}$$ = b (4.41)

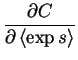$$\frac{\partial C }{ \partial \left< \exp s \right>}$$ = c. (4.42)