Addition and multiplication nodes can be used e.g. for constructing
affine transformations between the variables. Denoting the inputs by
sk, the output is
![]() for an addition node. The mean,
variance and expected exponential of the addition node are
for an addition node. The mean,
variance and expected exponential of the addition node are
![[*]](cross_ref_motif.gif) ),
(
),
(![[*]](cross_ref_motif.gif) ) and (
) and (![[*]](cross_ref_motif.gif) ). They are
). They are
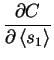 |
= | 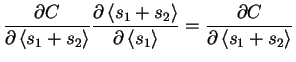 |
(4.27) |
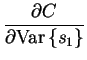 |
= | 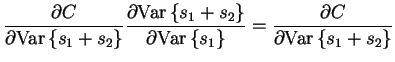 |
(4.28) |
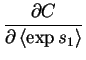 |
= | 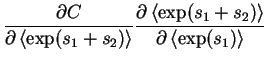 |
(4.29) |
| = | 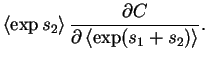 |
The equations for larger sums are obtained by induction, e.g. s1+s2+s3=(s1+s2)+s3.