



Next: Update Rule
Up: Building Blocks for Hierarchical
Previous: Building Blocks for Hierarchical
Gaussian Variables
A Gaussian variable s has two inputs m and v and prior
probability
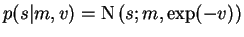 .
The variance is
parameterised this way because then the mean and expected exponential
of v suffice for computing the cost function. In Appendix A, it is
shown that when s, m and v are mutually independent, i.e.
q(s,
m, v) = q(s)q(m)q(v),
.
The variance is
parameterised this way because then the mean and expected exponential
of v suffice for computing the cost function. In Appendix A, it is
shown that when s, m and v are mutually independent, i.e.
q(s,
m, v) = q(s)q(m)q(v),
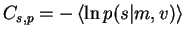 yields
yields
![\begin{displaymath}C_{s,p} = \frac{1}{2}\left\{ \left< \exp v \right>
\left[\le...
...\widetilde{s} \right] -
\left< v \right> + \ln 2\pi\right\} .
\end{displaymath}](img73.gif) |
(4.1) |
For observed variables this is the only term in the cost function but
for latent variables there is also Cs,q: the part resulting from
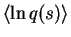 .
The posterior approximation q(s) is defined to
be Gaussian with mean
.
The posterior approximation q(s) is defined to
be Gaussian with mean
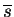 and variance
and variance
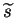 :
:
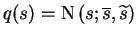 .
This yields
.
This yields
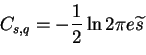 |
(4.2) |
which is the negative entropy of Gaussian variable with variance
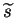 .
The parameters
.
The parameters
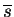 and
and
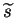 are to be optimised
during learning.
are to be optimised
during learning.
The output of a latent Gaussian node trivially provides expectation
and variance:
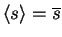 and
and
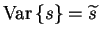 .
The
expected exponential is
.
The
expected exponential is
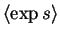 |
= |
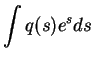 |
(4.3) |
| |
= |
![$\displaystyle \int (2\pi \widetilde{s})^{-1/2}\exp\left[\frac{-(s-\overline{s})^2}{2\widetilde{s}}+s\right]ds$](img83.gif) |
(4.4) |
| |
= |
![$\displaystyle \int (2\pi \widetilde{s})^{-1/2}\exp\left[\frac{-(s-\overline{s}-\widetilde{s})^2}{2\widetilde{s}}+\overline{s}+\frac{\widetilde{s}}{2}\right]ds$](img84.gif) |
(4.5) |
| |
= |
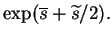 |
(4.6) |
The outputs of observed nodes are scalar values instead of
distributions and thus
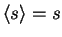 ,
,
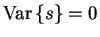 and
and
 .
.




Next: Update Rule
Up: Building Blocks for Hierarchical
Previous: Building Blocks for Hierarchical
Tapani Raiko
2001-12-10
![]() .
The variance is
parameterised this way because then the mean and expected exponential
of v suffice for computing the cost function. In Appendix A, it is
shown that when s, m and v are mutually independent, i.e.
q(s,
m, v) = q(s)q(m)q(v),
.
The variance is
parameterised this way because then the mean and expected exponential
of v suffice for computing the cost function. In Appendix A, it is
shown that when s, m and v are mutually independent, i.e.
q(s,
m, v) = q(s)q(m)q(v),
![]() yields
yields
![]() and
and
![]() .
The
expected exponential is
.
The
expected exponential is
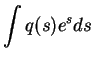
![$\displaystyle \int (2\pi \widetilde{s})^{-1/2}\exp\left[\frac{-(s-\overline{s})^2}{2\widetilde{s}}+s\right]ds$](img83.gif)
![$\displaystyle \int (2\pi \widetilde{s})^{-1/2}\exp\left[\frac{-(s-\overline{s}-\widetilde{s})^2}{2\widetilde{s}}+\overline{s}+\frac{\widetilde{s}}{2}\right]ds$](img84.gif)