
Next: Experiments
Up: Control Schemes
Previous: Optimistic Inference Control (OIC)
Nonlinear model predictive control (NMPC) [13] is based
on minimising a cost function 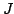 defined over a future window
of fixed length
defined over a future window
of fixed length 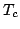 .
For example, the quadratic difference between the predicted future observations
.
For example, the quadratic difference between the predicted future observations
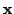 and a reference signal
and a reference signal
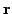 can be used:
can be used:
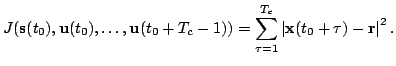 |
(9) |
Then 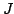 is minimised w.r.t. the control signals
is minimised w.r.t. the control signals
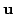 and the first one
and the first one
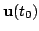 is executed.
In this paper, the states and observations (but not control signals) are
modelled probabilistically so we actually minimise the expected cost
is executed.
In this paper, the states and observations (but not control signals) are
modelled probabilistically so we actually minimise the expected cost
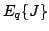 . The current guess
. The current guess
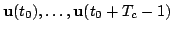 defines a probability
distribution over future states and observations. This inference can
be done with a single forward pass, when ignoring the
policy mapping, that is, the dependency of the state on future control signals.
In this case, it makes sense to ignore the policy mapping anyway,
since the future control signals do not have to follow the policy.
Minimisation of
defines a probability
distribution over future states and observations. This inference can
be done with a single forward pass, when ignoring the
policy mapping, that is, the dependency of the state on future control signals.
In this case, it makes sense to ignore the policy mapping anyway,
since the future control signals do not have to follow the policy.
Minimisation of 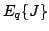 is done with a certain quasi-Newton
algorithm [12]. For that, the partial derivatives
is done with a certain quasi-Newton
algorithm [12]. For that, the partial derivatives
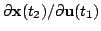 for all
for all
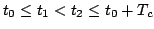 are computed efficiently based on the chain rule and
dynamic programming. Details are left for future publications due to lack of space.
The use of a cost function makes NMPC very versatile. Costs for control signals and
observations can be set for instance to restrict values within bounds
etc. Quadratic costs such as (9) make things easy for
the optimisation algorithm.
are computed efficiently based on the chain rule and
dynamic programming. Details are left for future publications due to lack of space.
The use of a cost function makes NMPC very versatile. Costs for control signals and
observations can be set for instance to restrict values within bounds
etc. Quadratic costs such as (9) make things easy for
the optimisation algorithm.
Table I:
Control Scheme Summary
| Scheme |
Based on |
Data |
Speed |
| DC |
internal MLP |
task-oriented |
fast |
| OIC |
probabilistic inference |
general |
slow |
| NMPC |
cost minimisation |
general |
slow |


Next: Experiments
Up: Control Schemes
Previous: Optimistic Inference Control (OIC)
Tapani Raiko
2005-05-23