
Next: Nonlinear Model Predictive Control
Up: Control Schemes
Previous: Direct Control (DC)
Optimistic Inference Control (OIC)
Optimistic inference control (OIC) is a novel method which works as
follows. Assume that after a fixed delay 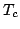 , the desired
goal is reached. That is, (some components of) the observations
, the desired
goal is reached. That is, (some components of) the observations
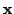 are at the desired
level
are at the desired
level
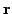 . Given this optimistic assumption and the
observations and control signals so far, infer what happens in between. Then
choose the expectation of
. Given this optimistic assumption and the
observations and control signals so far, infer what happens in between. Then
choose the expectation of
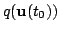 as before. An example situation is
illustrated in Figure 2.
as before. An example situation is
illustrated in Figure 2.
Figure 2:
Optimistic inference control (see Section III-B).
The inferred observations and control signals are plotted
with confidence intervals. The current time is
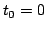 and after time
and after time
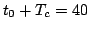 , the observation
, the observation
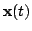 is assumed to be at the desired level
is assumed to be at the desired level
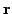 .
.
|
|
OIC in a nutshell:
Given observations
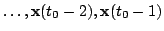 and
and
control signals
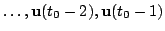
1: Fix future
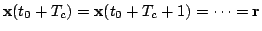
2: Infer the distribution
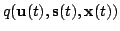 for all
for all 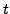
3: Select the mean of
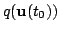 as the control signal
as the control signal
4: Observe
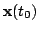 and release
and release
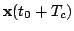
5: Increase 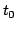 and loop from
and loop from 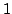
OIC propagates the same evidence forwards as the DC and
additionally, the evidence from the desired future backwards. The
inference is conceptually simple, but algorithmically difficult. The
information from the future needs to flow through tens of nonlinear
mappings
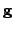 before it affects
before it affects
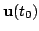 .
In case there are constraints for control signals or observations,
they are forced after every inference iteration. If the horizon is
set too short or the goal is otherwise overoptimistic, the method
becomes unreliable. Even with a realistic goal, it is not in general
guaranteed that the iteration will converge to the optimal control
signal, as the iteration may get stuck in a local minimum. The inferred
control signals can be validated by releasing the optimistic future and
re-inferring. If the future changes a lot, the control is unreliable.
Note that OIC does not require goal-oriented data, because different
goals can be set by changing the desired future.
.
In case there are constraints for control signals or observations,
they are forced after every inference iteration. If the horizon is
set too short or the goal is otherwise overoptimistic, the method
becomes unreliable. Even with a realistic goal, it is not in general
guaranteed that the iteration will converge to the optimal control
signal, as the iteration may get stuck in a local minimum. The inferred
control signals can be validated by releasing the optimistic future and
re-inferring. If the future changes a lot, the control is unreliable.
Note that OIC does not require goal-oriented data, because different
goals can be set by changing the desired future.


Next: Nonlinear Model Predictive Control
Up: Control Schemes
Previous: Direct Control (DC)
Tapani Raiko
2005-05-23
![\includegraphics[width=0.48\textwidth]{predictivecontrol.eps}](img51.gif)
![\includegraphics[width=0.48\textwidth]{predictivecontrol.eps}](img51.gif)
and
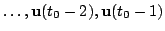
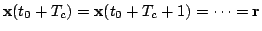
for all
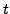
as the control signal
and release
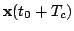
and loop from