Variational Bayesian (VB) learning provides even stronger tools
against overfitting. VB version of PCA [10]
approximates the joint posterior of the unknown quantities using a
simple multivariate distribution. Each model parameter is described
a posteriori using independent Gaussian distributions:
![]() and
and
![]() , where
, where
![]() and
and
![]() denote the mean of the solution and
denote the mean of the solution and
![]() and
and
![]() denote the variance of each
parameter. The means
denote the variance of each
parameter. The means
![]() ,
,
![]() can then be used as
point estimates of the parameters while the variances
can then be used as
point estimates of the parameters while the variances
![]() ,
,
![]() define the reliability of the estimates (or credible
regions). The direct extension of the method in [10]
to missing values can be computationally very demanding. VB-PCA has
been used to reconstruct missing values in [11,12]
with algorithms that complete the data matrix, which is also very
inefficient in case a large part of data is missing. In this article,
we implement VB learning using a gradient-based procedure similar to
the subspace learning algorithm described in Section 3.
define the reliability of the estimates (or credible
regions). The direct extension of the method in [10]
to missing values can be computationally very demanding. VB-PCA has
been used to reconstruct missing values in [11,12]
with algorithms that complete the data matrix, which is also very
inefficient in case a large part of data is missing. In this article,
we implement VB learning using a gradient-based procedure similar to
the subspace learning algorithm described in Section 3.
By applying the framework described in [12] to the model in Eqs. (7-8), the cost function becomes:
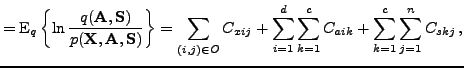 |
(10) |
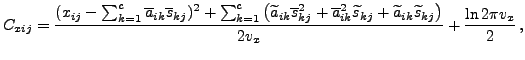 |
|
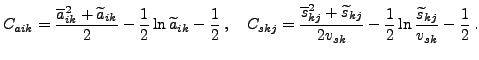 |
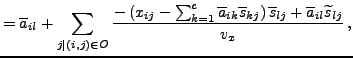 |
(12) | |
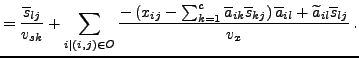 |
(13) |