Let us consider the same problem when the data matrix has missing
entries. We would like to find
![]() and
and
![]() such that
such that
![]() for the observed data samples. The rest of the product
for the observed data samples. The rest of the product
![]() represents the reconstruction of missing values.
represents the reconstruction of missing values.
The subspace learning algorithm works in a straightforward manner also
in the presence of missing values. We just take the sum over only
those indices ![]() and
and ![]() for which the data entry
for which the data entry ![]() (the
(the
![]() th element of
th element of
![]() ) is observed, in short
) is observed, in short
![]() . The cost
function is
. The cost
function is
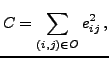 with with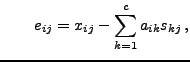 |
(3) |
We propose to use a speed-up to the gradient descent algorithm. In
Newton's method for optimization, the gradient is multiplied by the
inverse of the Hessian matrix. Newton's method is known to be
fast-converging, but using the full Hessian is computationally costly
in high-dimensional problems (![]() ). Here we use only the
diagonal part of the Hessian matrix, and include a control parameter
). Here we use only the
diagonal part of the Hessian matrix, and include a control parameter
![]() that allows the learning algorithm to vary from the standard
gradient descent (
that allows the learning algorithm to vary from the standard
gradient descent (![]() ) to the diagonal Newton's method
(
) to the diagonal Newton's method
(![]() ). The final learning rules then take the form
). The final learning rules then take the form
For comparison, we also consider two alternative PCA methods that can be adapted for missing values.