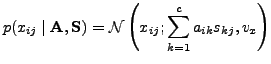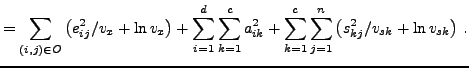Next: Variational Bayesian Learning
Up: Overfitting in PCA
Previous: Overfitting in PCA
Regularization
A popular way to regularize ill-posed problems is penalizing the use
of large parameter values by adding a proper penalty term into the
cost function. This can be obtained using a probabilistic formulation
with (independent) Gaussian priors and a Gaussian noise model:
The cost function (ignoring constants) is minus logarithm of the
posterior of the unknown parameters:
The cost function can be minimized using a gradient-based approach as
described in Section 3. The corresponding update rules
are similar to (5)-(6)
except for the extra terms which come from the prior.
Note that in case of joint optimization of
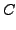 BR w.r.t.
BR w.r.t. 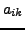 ,
, 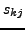 ,
, 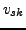 , and
, and 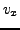 , the cost function
(9) has a trivial minimum with
, the cost function
(9) has a trivial minimum with 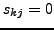 ,
,
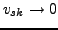 . We try to avoid this minimum by using an
orthogonalized solution provided by unregularized PCA for
initialization. Note also that setting
. We try to avoid this minimum by using an
orthogonalized solution provided by unregularized PCA for
initialization. Note also that setting 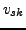 to small values for
some components
to small values for
some components 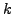 is equivalent to removal of irrelevant components
from the model. This allows for automatic determination of the proper
dimensionality
is equivalent to removal of irrelevant components
from the model. This allows for automatic determination of the proper
dimensionality 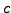 instead of discrete model comparison (see, e.g.,
[10]).
instead of discrete model comparison (see, e.g.,
[10]).



Next: Variational Bayesian Learning
Up: Overfitting in PCA
Previous: Overfitting in PCA
Tapani Raiko
2007-07-16