![[*]](cross_ref_motif.gif) . The part of the cost function C defined in
(
. The part of the cost function C defined in
(![[*]](cross_ref_motif.gif) ) that corresponds to the variable is derived here.
The posterior approximations of
s, m and v are mutually independent
) that corresponds to the variable is derived here.
The posterior approximations of
s, m and v are mutually independent
A node called the Gaussian variable was presented in
Section ![[*]](cross_ref_motif.gif) . The part of the cost function C defined in
(
. The part of the cost function C defined in
(![[*]](cross_ref_motif.gif) ) that corresponds to the variable is derived here.
The posterior approximations of
s, m and v are mutually independent
) that corresponds to the variable is derived here.
The posterior approximations of
s, m and v are mutually independent
| q(s,m, v) = q(s)q(m)q(v) | (10.1) |
| (10.2) |
The first part Cp defined in (![[*]](cross_ref_motif.gif) ) is addressed first.
) is addressed first.
We still need to compute the expectation of (s-m)2
![[*]](cross_ref_motif.gif) ) by (
) by (![[*]](cross_ref_motif.gif) ) yields (
) yields (![[*]](cross_ref_motif.gif) ):
):
| (10.12) |
The second part of the cost function Cq defined in (![[*]](cross_ref_motif.gif) )
is
)
is
| Cs,q | = | (10.13) | |
| = | (10.14) | ||
| = | ![$\displaystyle \left< \ln \left[(2\pi \widetilde{s})^{-1/2}\exp \frac{-(s-\overline{s})^2}{2\widetilde{s}}\right] \right>$](img267.gif) |
(10.15) | |
| = | 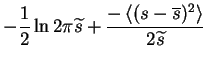 |
(10.16) | |
| = | 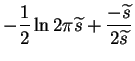 |
(10.17) | |
| = | 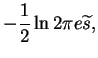 |
(10.18) |
![[*]](cross_ref_motif.gif) ).
).