![[*]](cross_ref_motif.gif) . It is a minimisation problem for the cost
function
Cf=Cf,p+Cf,q. Here is a proof that each iteration
decreases the cost function (or keeps it the same if the partial
derivatives vanish).
. It is a minimisation problem for the cost
function
Cf=Cf,p+Cf,q. Here is a proof that each iteration
decreases the cost function (or keeps it the same if the partial
derivatives vanish).
The update rule for the nonlinear node is considered in
Section ![[*]](cross_ref_motif.gif) . It is a minimisation problem for the cost
function
Cf=Cf,p+Cf,q. Here is a proof that each iteration
decreases the cost function (or keeps it the same if the partial
derivatives vanish).
. It is a minimisation problem for the cost
function
Cf=Cf,p+Cf,q. Here is a proof that each iteration
decreases the cost function (or keeps it the same if the partial
derivatives vanish).
A different notation is used here.
The quadratic term
![]() is taken into account by first finding an optimal expected value of
f marked with
is taken into account by first finding an optimal expected value of
f marked with
![]() and the variance
and the variance
![]() that
corresponds to how much difference will cost.
that
corresponds to how much difference will cost.
| = | (2b)-1 | (11.1) | |
| = | (11.2) |
| (11.3) | |||
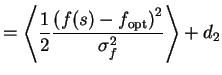 |
(11.4) |
Now all the affected terms of C can be written as
| = | 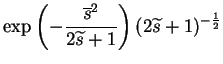 |
(11.7) | |
| = | 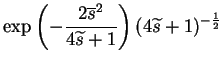 |
(11.8) |
Now we have to find
![]() and
and
![]() such that
Cf=Cf,p+Cf,q is minimized. The partial derivates of Cfare
such that
Cf=Cf,p+Cf,q is minimized. The partial derivates of Cfare
It is worthwhile to note the connection derived from (![[*]](cross_ref_motif.gif) )
and (
)
and (![[*]](cross_ref_motif.gif) ):
):
For
![]() ,
a gradient descent is used with the step length
approximated from Newton's method. The approximation composed from
(
,
a gradient descent is used with the step length
approximated from Newton's method. The approximation composed from
(![[*]](cross_ref_motif.gif) )
)
As was shown, these steps guarantee a direction, in which the cost function decreases locally. If the derivatives are zero, the iterating has converged. To guarantee also that the cost function does not increase because of a too long step, the update candidates are verified. The step is halved as long as the cost is about to rise.