Adjustment

An essential part of the method is the iterative adjustment of the posterior approximation. Learning takes place when adjusting the network part by part using the update rules defined in Chapter . There are two implementations of the algorithm that differ at this point. In the Matlab version, vectors s_i and u_i, matrices A_i and B_i and parameter vectors like $\boldsymbol{\mu}_{s,i}$ are updated one at a time keeping all other parts constant. In the C++-version every node is updated by itself keeping all other nodes constant. Updating many nodes at one time requires some further considerations [44]. The actual experiments were run using the Matlab version.

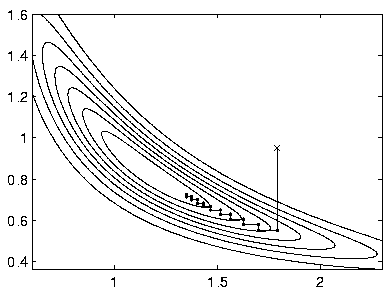
Alternating updating is the method that is used in this thesis, but it is not the only option. Figure  shows a simple example, where it is not very effective, since it leads to a zig-zag path. One option could be to sweep through many updates once and then optimise the length of the step in the direction of the whole sweep. This is further discussed in Chapter .

  

Figure: The posterior probability density of a simple problem: $x=s_1 s_2 + n, x=1, p(s_k)=\operatorname{N}\left(s_k;0,k\right), p(n) = \operatorname{N}\left(n;0,0.02\right)$. The density forms a ridge and the ascent for finding an MAP solution is not very effective, if the parametrisised distributions of s₁ and s₂ are updated alternately.

The alternating adjustment can be compared to the expectation maximisation (EM) algorithm [13]. The EM algorithm alternates between two types of adjustment steps in which the other part is kept constant.