Discussion

The aim of this work was to build a model which could be used to find out statistical features in data in an unsupervised manner. Many of the previously presented methods scale poorly with respect to the number of intrinsic dimensions in the data or cannot take into account nonlinear effects. A model called hierarchical nonlinear factor analysis with variance modelling (HNFA+VM) is proposed.

The commonly used maximum likelihood (ML) and maximum a posteriori (MAP) learning criteria suffer from overfitting and thus cannot be used with nonlinear factor analysis models. A Bayesian approach based on sampling would be too slow for large problems. Ensemble learning is a good compromise between them and was therefore selected.

The complicated model is built from simple blocks which reduces the effort of implementation and increases extensibility. All computations are local which results in linear computational complexity. The idea for the structure of the model originates from nonlinear factor analysis (NFA) [43]. The computational or hidden units are replaced by latent variables. The same blocks can also be used to model variances which has been found important for analysis of image data [67,30].

The proposed learning algorithm for HNFA+VM was shown to be able to learn the structure of the underlying artificial but complicated process that generated the data. The experiments with real world data are not yet very convincing but it seems that introducing sparse connectivity could enhance the results significantly.

The computational complexity of the learning algorithm for HNFA+VM is linear with respect to the number of connections, sample vectors and sweeps. Still, the experiment with image data took more than a week to run with the Matlab version. A more efficient C++ version of the algorithm has become ready while writing this. It is also more flexible for example by allowing the pruning of single connections instead of whole neurons.

A sparse prior for the weights is likely to prove useful in many cases. On the first layer of the image experiments it would encourage local features to be formed in a patch. On the upper layer it would encourage the formation of complex-cell-like [30,29] sources as each of them typically models the variance of only a small number of the lower-level sources. The connections that are practically zero can be pruned away to make the algorithm significantly more efficient.

The number of time indices or observations is also crucial to the efficiency. When looking at a picture or a view, the human eye focuses in places of interests and not randomly. Perhaps a smaller set of data would suffice for interesting results if the data set would be selected in the same manner. Also, the rebooting and changing the data that is used should be studied more. There might be ways to take into account that the data has been changed. In case of online learning, one can use new data all the time. It is easy to use online learning with Bayesian methods. Preliminaly results with it are promising.

The learning with alternating adjustment is inefficient in cases where different parts can compensate each other. For finding the best rotation matrix, one should be able to adjust several parts of the model at once. To use a different part of the nonlinear function to get a different curvature, one should be able to compensate the affected scaling and bias terms at the same time. A resulting zig-zag path illustrated in Figure  leads to the right direction but very slowly. One could identify internally related groups of parameters whose adjustments are steady between sweeps and then make a one-dimensional optimisation along the direction of these steady updates. This could dramatically decrease the number of required sweeps. The system could also be made to predict which kinds of updates are the most effective ones.

The building blocks discussed in this thesis together with two more blocks presented in [66] can be used to build a wide variety of models. An important future line of research will be the automated construction of the model. The search through different model structures is facilitated by the ability of ensemble learning to automatically shut down parts of the model. The cost function can be used to determine wheather a modification of the structure is useful or not. The rate of decrease of the cost can be used to estimate the utility of further sweeps.

The building blocks can be connected to other time instances thus modelling the nonlinear dynamics of the sources. Valpola got good results [65,63] using nonlinear factor analysis with another nonlinear mapping from sources at time t to sources at time t+1. With image data, this would mean that in an animation the higher level sources would change slowly. This would encourage them to represent features that are for example translationally more or less invariant since an animation typically looks like a translation locally. This is promising, since some of the higher level sources did activate for example different horizontal edge features even with the static images.

Externally the variance neurons appear as any other Gaussian nodes. It is therefore easy to build also dynamic models for the variance. These kinds of models can be expected to be useful in many domains. For example volatility in financial markets is known to have temporal auto-correlations.

The scope of this thesis was restricted to models with purely local computations. In some cases it may be necessary to use models where a group of simple elements is treated as a single element whose external computations are local but whose internal computations may be more complex. The practical consequences of using a latent variable instead of a computational node in NFA should be studied.

The benefits of the proposed method are as follows. First, the method is unsupervised, that is, the learning does not require a teacher or human intervention. Second, the proposed structure is quite rich. It is not restricted to linear manifolds, it includes the modelling of the variance and the number of layers in the hierarchy is not restricted. Third, the computational complexity of the algorithm scales linearly with respect to the size of the problem, which means that the scalability is very good. Fourth, the method avoids overfitting which leads to good generalisation capability and requires no cross-validation. Finally, different model structures can be compared simply by using the cost function.

The restrictions of the method at its current state include the requirement of expertise in selecting preprocessing, initialisation, and the learning procedure since it is prone to local minima. The algorithm is computationally intensive compared to other simpler methods. A universal data analysis method should also be able to use data in other forms than just continuous valued vectors with constant number of dimensions. At least discrete values and relations to other observations would be useful. For example, real medical databases contain a mixture of measurements, natural language, images and relations to hospitals, doctors and treatments.

The assumption that the data is continuous valued is seldom exactly true. Even if the underlying phenomenon is continuous, the data might be more or less discrete. Prices tend to be rounded. Ages are typically given in full years. Digital images are typically discretised to for example 256 gray-scale values. These artefacts can cause unwanted phenomena in learning. They can be avoided by adding a small amount of random noise to the data set as was done in the experiments here. It would also be possible to add the noise implicitly by giving a virtual posterior variance for the observed samples. This idea is left for further studies.

The proposed model can be used to statistical analysis of data. It can be used to reconstruct missing values and thus to make predictions. The found sources can be used as features for other machine learning methods. The method can be further developed to be an artificial intelligence system. A concrete example application with images is visualised in Figure . Superresolution images can be obtained by adding extra pixels in between the original ones and considering them as missing values. The model could then reconstruct them in a manner explained in [57].

  

Figure: A statistical model of natural images can be used to form a superresolution image. It can be done by considering the pixels marked with ``M'' missing and reconstructed by the model.

Real applications with image data require the use of images much larger than 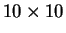$10 \times 10$ pixels. Even if the algorithm scales linearly, it would be reasonable to explicitly take into account the translational invariance in images. One could start the learning process with smaller patches and use the results as an initialisation for learning with larger patches. The computationally expensive lowermost layers would be thus learned with smaller patches and the upper layers could combine the local features of them later on.

The effect of the initialisation on the final results should be studied. It seems that different kinds of initialisations result in different kinds of models. Therefore different methods for initialisation should be tested for different kinds of data. One of the methods that could be good for initialisation, is the nonlinear component analysis (NCA) [60], which would differ from the methods used so far by being nonlinear.

Scaling of the model vectors in the initialisation requires some more attention. By comparing the initial scales to the resulting model, one can find a more appropriate scaling factor 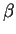$\beta$ which could later be used for a better initialisation and thus faster convergence. Another option would be to project the data to a model vector and compare the resulting distribution to one given by a nonlinear unit. A good scaling factor would be one that matches the distributions best.

The C++-version of the algorithm allows the connections to be made more freely. One could connect the upper layers directly to the lower layers in addition to using layers in between. This could decrease the effect of a particular initialisation method.