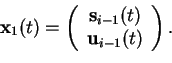Initialisation

The network is initialised as a single layer, that is n=1. This means that there are only variance neurons connected to the observations. A new layer i>1 can be added during the learning. The means of matrixes A_i-1 and B_i-1 are initialised by applying vector quantisation [1] to the whitened mean of concatenated vectors s_i-1(t) and u_i-1(t)

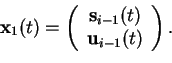$$\mathbf{x}_1(t) = \left( \begin{array}{c}\mathbf{s}_{i-1}(t) \\ \mathbf{u}_{i-1}(t) \end{array} \right).$$ (6.1)

The whitened vector x₂(t) of x₁(t) is obtained from singular value decomposition

x₂(t) = D^-1/2Vx₁(t), (6.2)

where V contains the orthonormal eigenvectors of the covariance matrix of x₁(t) and D is the diagonal matrix of its eigenvalues. Each x₂(t) is matched to one of the normalised model vectors M_k

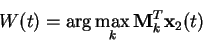$$W(t) = \arg \max_k \mathbf{M}_k^{T}\mathbf{x}_2(t)$$ (6.3)

and the model vector is moved to the mean of the vectors x₂(t) that are matched to it

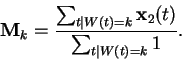$$\mathbf{M}_k = \frac{\sum_{t\mid W(t)=k} \mathbf{x}_2(t)}{\sum_{t\mid W(t)=k} 1}.$$ (6.4)

Finally the initial values for A_i-1 and B_i-1 are

$$\left( \begin{array}{c}\mathbf{A}_{i-1} \\ \mathbf{B}_{i-1} \... ...rray} \right) = \beta \mathbf{V}^T\mathbf{D}^{1/2}\mathbf{M}.$$ (6.5)

The scaling factor $\beta$ should be selected such that the corresponding sources would operate in an appropriate range. Here the value $\beta=2$ was used. It means that f(s_i) = 1 corresponds to twice the length of a model vector. The selection is further discussed in Chapter .

The posterior means of sources s_i(t) were initialised to -2 and the means of u_i(t) were initialised to -1. These very simple initial values of the sources are not harmful, because of a special state explained in Section . The posterior variances of s_i(t), u_i(t), A_i-1 and B_i-1 are initialised to small values.