![[*]](cross_ref_motif.gif) . The scalar
observed data x(t) is a Gaussian variable with prior mean m and
prior variance
. The scalar
observed data x(t) is a Gaussian variable with prior mean m and
prior variance
The purpose of this first example is to illustrate what is meant with
the propagation of expected values and derivatives. The model
structure is shown in Figure ![[*]](cross_ref_motif.gif) . The scalar
observed data x(t) is a Gaussian variable with prior mean m and
prior variance
. The scalar
observed data x(t) is a Gaussian variable with prior mean m and
prior variance ![]() :
:
| (4.10) |
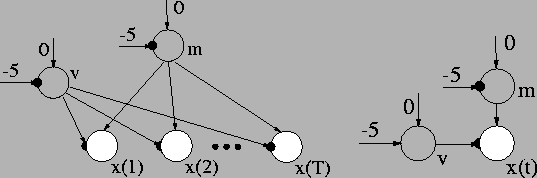 |
The model basically states that the data points are scattered with an
unknown mean and variance. They can be estimated from the data. An
estimate of the posterior distributions
![]() and
and
![]() are
are
| (4.13) | |||
| (4.14) |
The expected value and the variance are required from the prior mean m of x(t). The expected value and the expected exponential are required from the variable v that determines the prior variance of x(t). The outputs of Gaussian variables can provide all of these expected values.
The learning would start with some initial values, say
![]() ,
,
![]() ,
,
![]() and
and
![]() .
The cost concerning the
observations x(t) from (
.
The cost concerning the
observations x(t) from (![[*]](cross_ref_motif.gif) ) is
) is
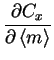 |
= | ![$\displaystyle \left< \exp v \right> \sum_{t=1}^T \left[\overline{m}-x(t)\right]$](img121.gif) |
(4.16) |
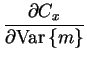 |
= | 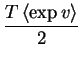 |
(4.17) |
The part of the cost function that concerns the variable m directly
has two parts simplified from Equations (![[*]](cross_ref_motif.gif) ) and
(
) and
(![[*]](cross_ref_motif.gif) )
)
| = | 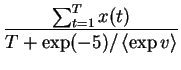 |
(4.20) | |
| = | 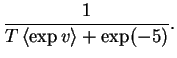 |
(4.21) |
From the result we can see that the mean of m is close to the mean
of the observations. The prior in (![[*]](cross_ref_motif.gif) ) pulls
it slightly towards zero. The uncertainty of the prior mean
) pulls
it slightly towards zero. The uncertainty of the prior mean
![]() does not directly depend on the actual data. When the number of
observations T increases, the uncertainty i.e. the posterior
variance
does not directly depend on the actual data. When the number of
observations T increases, the uncertainty i.e. the posterior
variance
![]() decreases towards zero.
decreases towards zero.
The partial derivatives of Cx defined in ![[*]](cross_ref_motif.gif) with respect
to v are
with respect
to v are
| = | ![$\displaystyle \sum_{t=1}^T \frac{1}{2}
\left[\left(x(t)-\overline{m}\right)^{2}+\widetilde{m}
\right]$](img132.gif) |
(4.22) | |
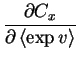 |
= | (4.23) |
![[*]](cross_ref_motif.gif) ) and
(
) and
(![[*]](cross_ref_motif.gif) ). Therefore, when optimising
). Therefore, when optimising
The optimal solution for q(m) depends on q(v) and vice versa. This means that to fully solve the problem, one could update q(m) and q(v) alternately.