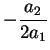Next: First Example
Up: Gaussian Variables
Previous: Gaussian Variables
The posterior distribution q(s) of a latent Gaussian node can be
updated as follows.
- 1.
- First, the gradients of Cp w.r.t.
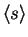 ,
,
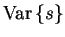 and
and
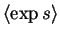 are computed.
are computed.
- 2.
- Second, the terms in Cp which depend on
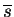 and
and
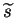 are
assumed to be
are
assumed to be
![$a \overline{s} + b [(\overline{s}-
\overline{s}_{\text{current}})^2 + \widetilde{s}] + c\left< \exp s \right> + d$](img92.gif) ,
where
,
where
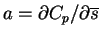 ,
,
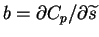 and
and
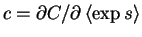 .
This is shown to be true in Section
.
This is shown to be true in Section ![[*]](cross_ref_motif.gif) .
.
- 3.
- Third, the
minimum of
Cs = Cs,p + Cs,q is solved.
The cost function is written explicitely as the function of
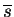 and
and
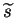 :
:
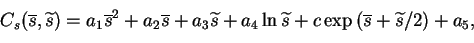 |
(4.7) |
where a1 > 0 and a4 < 0. First,
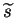 is kept
constant and
the optimal
is kept
constant and
the optimal
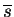 is solved using Newton's iteration. Then the
optimal
is solved using Newton's iteration. Then the
optimal
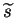 is solved using a stabilised fixed-point iteration
and keeping
is solved using a stabilised fixed-point iteration
and keeping
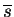 constant.
constant.
In the special case c=0,
the minimum of
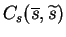
can be found analytically. In this case, q(s) is optimal among all
functions i.e. the free-form approximation.




Next: First Example
Up: Gaussian Variables
Previous: Gaussian Variables
Tapani Raiko
2001-12-10
![[*]](cross_ref_motif.gif) .
.
![[*]](cross_ref_motif.gif) .
.
![]() and
and
![]() :
:
![]()