Generalisation

A learning algorithm is said to overlearn the training data set, when its performance with test data starts to get worse during the learning with training data. The system starts to lose its ability to generalise. The same can happen when increasing the complexity of the model. The model is said to overfit to the data. When the model is too simple or the learning is stopped too early, the problem is called underfitting or underlearning accordingly. Balancing between over- and underfitting has perhaps been the main difficulty in model building.

There are ways to fight overfitting and overlearning [24,5,9]. Weight decay [41] for MLP networks corresponds to moving from ML to MAP solution in Figure . It punishes the model for using large values for weights and thus makes the mapping smoother. The same idea can be taken further - one can do model selection with MAP estimates by introducing a heuristical punishment term for model complexity. A popular and less heuristic method to select the best time to stop learning or the best complexity of a model is the cross-validation [24]. Part of the training data is left for validation and the models are compared based on their performance with the validation set.

Bayesian learning solves the tradeoff between under- and overfitting. If one has to select a single value for the parameter vector, it should represent the posterior probability mass well. The MAP solutions are attracted to high but sometimes narrow peaks. Figure  shows a situation, where search for the MAP solution first finds a good representative, but then moves to the highest peak which is on the border. This type of situation seems to be very common and the effect becomes stronger, when the dimensionality of the parameter space increases.

  

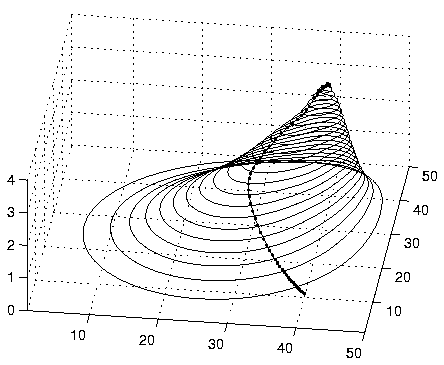
Figure 3.2: A hypothetical posterior pdf. A point estimate could first find a good representative of the probability mass, but then overfit to a narrow peak.

Because the KL divergence involves an expectation over a distribution, it is sensitive to the probability mass rather than to the probability density. Therefore ensemble learning is not attracted so much to narrow peaks and overfitting is largely avoided. Experiments have shown [57] that ensemble learning performs well in generalisation.

Two example cases are described in the following Sections. In the first simple case, it is sufficient to use MAP estimate instead of ML to avoid overfitting. In the second example, however, both of the point estimates fail.