



Next: Role of Prior Information
Up: Generalisation
Previous: An Example on Polynomial
Example Where Point Estimates Fail
The following example illustrates what can go wrong with point
estimates. Three dimensional data vectors
x(t) are modelled
with linear factor analysis
using a single source s(t). The weight matrix
A might get a
value
![\begin{displaymath}\mathbf{A} = \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right],
\end{displaymath}](img61.gif) |
(3.16) |
while the source can just copy the values of the first dimension of
x(t)
The noise model is Gaussian with zero mean and parameterised variance
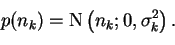 |
(3.18) |
When the reconstruction error or the noise term is evaluated
![\begin{displaymath}\mathbf{n}(t) = \mathbf{x}(t)- \mathbf{A}s(t) = \left[ \begin{array}{c} 0 \\ x_2(t) \\ x_3(t) \end{array} \right],
\end{displaymath}](img63.gif) |
(3.19) |
one can see that problems will arise with the first variance parameter
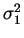 .
The likelihood of the data
.
The likelihood of the data
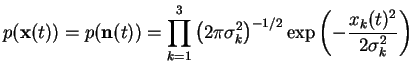 |
|
|
(3.20) |
![$\displaystyle = \left[\frac{1}{\sqrt{2 \pi}}\prod_{k=2}^3 \left(2\pi \sigma_k^2...
...)^{-1/2}\exp\left(-\frac{x_k(t)^2}{2\sigma_k^2}\right)\right]\frac{1}{\sigma_1}$](img66.gif) |
|
|
(3.21) |
goes to infinity when the variance
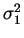 goes to zero. Same
applies to the posterior density, since it is basically just the
likelihood multiplied by a finite factor.
goes to zero. Same
applies to the posterior density, since it is basically just the
likelihood multiplied by a finite factor.
The found model is completely useless and still, it is rated as
infinitely good using point estimates. These problems are typical for
models with estimates of the noise level or products. They can be
sometimes avoided by fixing the noise level or using certain
normalisations [2].




Next: Role of Prior Information
Up: Generalisation
Previous: An Example on Polynomial
Tapani Raiko
2001-12-10
![\begin{displaymath}\mathbf{A} = \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right],
\end{displaymath}](img61.gif)
![\begin{displaymath}\mathbf{A} = \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right],
\end{displaymath}](img61.gif)
![\begin{displaymath}\mathbf{n}(t) = \mathbf{x}(t)- \mathbf{A}s(t) = \left[ \begin{array}{c} 0 \\ x_2(t) \\ x_3(t) \end{array} \right],
\end{displaymath}](img63.gif)
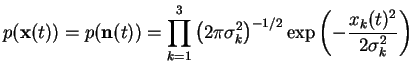
![$\displaystyle = \left[\frac{1}{\sqrt{2 \pi}}\prod_{k=2}^3 \left(2\pi \sigma_k^2...
...)^{-1/2}\exp\left(-\frac{x_k(t)^2}{2\sigma_k^2}\right)\right]\frac{1}{\sigma_1}$](img66.gif)