The data set
X consists of 10 points on a plane. Model
![]() states, that the points have been generated by a sixth order
polynomial, whose weights are drawn from a Gaussian distribution with
a zero mean and standard deviation (std) 2 and a Gaussian noise with
std 0.1 is added. The problem is to find these weights.
states, that the points have been generated by a sixth order
polynomial, whose weights are drawn from a Gaussian distribution with
a zero mean and standard deviation (std) 2 and a Gaussian noise with
std 0.1 is added. The problem is to find these weights.
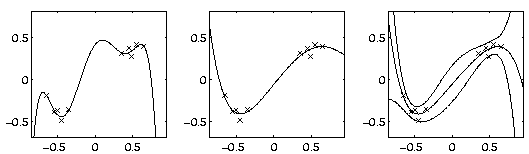
Figure ![[*]](cross_ref_motif.gif) shows the results. There are many different
polynomials that fit quite well to the data. The ML solution does the
fitting best, but the weights of the polynomial are large and the
polynomial has a complicated form. The MAP solution takes the prior
distributions into account, and the result is smoother. Bayesian
learning takes into account all polynomials and weights them with
their posterior probability. It solves the tradeoff between under- and
overfitting. Note that the error fractiles are closer in the parts of
the polynomial that have data points.
shows the results. There are many different
polynomials that fit quite well to the data. The ML solution does the
fitting best, but the weights of the polynomial are large and the
polynomial has a complicated form. The MAP solution takes the prior
distributions into account, and the result is smoother. Bayesian
learning takes into account all polynomials and weights them with
their posterior probability. It solves the tradeoff between under- and
overfitting. Note that the error fractiles are closer in the parts of
the polynomial that have data points.
 |