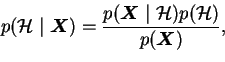Model Selection

Ensemble learning offers another important benefit. Comparison of different models is straightforward. The Bayes rule can be applied again to get the probability of a model given the data

$$p(\mathcal{H}\mid \boldsymbol{X}) = \frac{p(\boldsymbol{X}\mid \mathcal{H})p(\mathcal{H})}{p(\boldsymbol{X})},$$ (3.13)

where $p(\mathcal{H})$ is the prior probability of a model and p(X) is the probability of the data, which is constant. A lower bound on the evidence term $p(\boldsymbol{X}\mid \mathcal{H})$ is obtained from ()

$$p(\mathbf{X}\mid \mathcal{H}) = \exp(C_{\mathrm{KL}}- C) \geq \exp (-C)$$ (3.14)

Multiple models can be used as a mixture of experts model [24]. The experts can be weighted with their probabilities given in equation (). If the models have equal prior probabilities and the parameter approximations C_KL are equally good, the weights simplify to $\exp (-C)$. In practice, the costs tend to differ in the order of hundreds or thousands, which makes the model with the lowest cost C dominant. Therefore it is reasonable to concentrate on model selection rather than weighting.