


Next: Newton iteration for the
Up: Building Blocks for Variational
Previous: APPENDICES
Updating 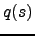 for the Gaussian node
for the Gaussian node
Here we show how to minimise the function
![$\displaystyle {\cal C}(m,v) = Mm + V[(m-m_0)^2 + v] + E \exp(m+v/2) - \frac{1}{2} \ln v,$](img314.png) |
(54) |
where 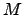 ,
,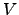 ,
,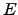 , and
, and 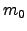 are scalar constants.
A unique solution exists when
are scalar constants.
A unique solution exists when 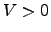 and
and 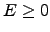 . This problem
occurs when a Gaussian posterior with mean
. This problem
occurs when a Gaussian posterior with mean 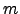 and variance
and variance 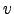 is
fitted to a probability distribution whose logarithm has both a
quadratic and exponential part resulting from Gaussian prior and
log-Gamma likelihoods, respectively, and Kullback-Leibler divergence
is used as the measure of the misfit.
is
fitted to a probability distribution whose logarithm has both a
quadratic and exponential part resulting from Gaussian prior and
log-Gamma likelihoods, respectively, and Kullback-Leibler divergence
is used as the measure of the misfit.
In the special case 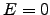 , the minimum of
, the minimum of
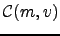 can be found
analytically and it is
can be found
analytically and it is
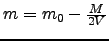 ,
,
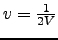 .
In other cases where
.
In other cases where 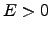 , minimisation is performed iteratively. At
each iteration, one Newton iteration for the mean
, minimisation is performed iteratively. At
each iteration, one Newton iteration for the mean 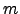 and one
fixed-point iteration for the variance
and one
fixed-point iteration for the variance 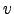 are carried out as
explained in more detail in the following.
are carried out as
explained in more detail in the following.
Subsections
Tapani Raiko
2006-08-28
![]() , the minimum of
, the minimum of
![]() can be found
analytically and it is
can be found
analytically and it is
![]() ,
,
![]() .
In other cases where
.
In other cases where ![]() , minimisation is performed iteratively. At
each iteration, one Newton iteration for the mean
, minimisation is performed iteratively. At
each iteration, one Newton iteration for the mean ![]() and one
fixed-point iteration for the variance
and one
fixed-point iteration for the variance ![]() are carried out as
explained in more detail in the following.
are carried out as
explained in more detail in the following.