Building Blocks

In this section we introduce the building blocks and equations for computation with them. The building blocks consist of variable nodes and computation nodes. The symbols we use for them are shown in Figure 1. We shall refer to inputs and outputs of the nodes. For variable nodes, input means a value which is used for the prior distribution and output is the value of the variable. For computation nodes, output is a fixed function of the inputs.

The variable nodes can be either continuous valued with Gaussian prior models or discrete with soft-max prior models. Gaussian and soft-max are chosen because the outputs of the Gaussian nodes can be used as inputs to Gaussian or soft-max nodes as will be explained shortly. This makes the nodes compatible with each other. Each variable can be either observed or latent.

Since the variable nodes are probabilistic, the values propagated between the nodes have distributions. When ensemble learning together with a factorial posterior approximation is used, the cost function can be computed by propagating certain expected values instead of full distributions. Consequently the cost function can be minimised based on gradients w.r.t. these expectations computed by back-propagation.

The input for prior mean of a Gaussian node requires the mean and variance. With a suitable parametrisation, mean and expected exponential are required from the input for prior variance. The output of a Gaussian node can provide the mean, variance and expected exponential and can thus be used as an input to both the mean and variance of another Gaussian node. Gaussian nodes are suitable parents for discrete nodes as well since soft-max requires the mean and expected exponential of the input. The expectations required by the inputs and provided by the outputs of different nodes are listed below:

Output provides:
Gaussian	$\left< \cdot \right>$	$\mathrm{Var}\left\{\cdot\right\}$	$\left< \exp\cdot \right>$
Gaussian with nonlinearity	$\left< \cdot \right>$	$\mathrm{Var}\left\{\cdot\right\}$
addition	$\left< \cdot \right>$	$\mathrm{Var}\left\{\cdot\right\}$	$\left< \exp\cdot \right>$
multiplication	$\left< \cdot \right>$	$\mathrm{Var}\left\{\cdot\right\}$
switch	$\left< \cdot \right>$	$\mathrm{Var}\left\{\cdot\right\}$	$\left< \exp\cdot \right>$
Prior for variable nodes requires:
mean of Gaussians	$\left< \cdot \right>$	$\mathrm{Var}\left\{\cdot\right\}$
variance of Gaussians	$\left< \cdot \right>$		$\left< \exp\cdot \right>$
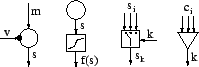soft-max of discrete	$\left< \cdot \right>$		$\left< \exp\cdot \right>$

Figure 1: First from left: A Gaussian latent variable $s$, marked with a circle, has a prior mean $m$ and a prior variance $\exp(-v)$. Second: A nonlinearity $f$ is applied immediately after a Gaussian variable. Third: A switch selects the $k$th continuous valued input as the output. Fourth: Discrete variable $k$, marked with a triangle, has a soft-max prior derived from continuous valued variables $c_{i}$.