The prior probabilities of discrete variables with ![]() possible values
can be assigned from
possible values
can be assigned from ![]() continuous valued signals
continuous valued signals ![]() using
soft-max prior:
using
soft-max prior:
| (10) |
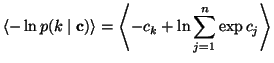 |
(11) | ||
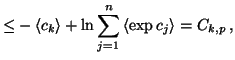 |
(12) |
For latent discrete variables there are no restrictions to the
posterior approximation ![]() . The term
. The term ![]() in the cost
function arising from
in the cost
function arising from
![]() is simply the negative
entropy of
is simply the negative
entropy of ![]() .
.
The update of ![]() is analogous to Gaussian variables: the gradient
of
is analogous to Gaussian variables: the gradient
of ![]() w.r.t. the vector
w.r.t. the vector ![]() with
with
![]() is
assumed to arise from a linear term
is
assumed to arise from a linear term
![]() ,
where
,
where
![]() denotes the value of
denotes the value of ![]() assuming that
assuming that
![]() . The linearity assumption holds exactly if the value of the
discrete node propagates only to Gaussian variables (through switches)
and corresponds to an upper bound of the cost function if the values
are used by other discrete variables with soft-max prior. It can be
shown that at the minimum of the cost function it holds
. The linearity assumption holds exactly if the value of the
discrete node propagates only to Gaussian variables (through switches)
and corresponds to an upper bound of the cost function if the values
are used by other discrete variables with soft-max prior. It can be
shown that at the minimum of the cost function it holds
![]() .
.