

Next: Gaussian variable with nonlinearity
Up: Building Blocks
Previous: Gaussian variables
Addition and multiplication nodes can be used e.g. for constructing
linear mappings and affine transformations between the variables.
Denoting the inputs by 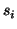 , the outputs are
, the outputs are
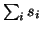 for
addition and
for
addition and
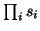 for multiplication nodes. The mean,
variance and expected exponential of the addition node are
for multiplication nodes. The mean,
variance and expected exponential of the addition node are
assuming 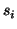 independent. For a multiplication node, the expected
exponential cannot be evaluated without knowing the exact distribution
of the inputs. Assuming independence between
independent. For a multiplication node, the expected
exponential cannot be evaluated without knowing the exact distribution
of the inputs. Assuming independence between 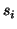 , the mean and the
variance of the output are
, the mean and the
variance of the output are
The equations for larger sums or products are obtained by induction,
e.g.
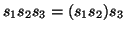 .
.


Next: Gaussian variable with nonlinearity
Up: Building Blocks
Previous: Gaussian variables
Harri Valpola
2001-10-01
![]() , the outputs are
, the outputs are
![]() for
addition and
for
addition and
![]() for multiplication nodes. The mean,
variance and expected exponential of the addition node are
for multiplication nodes. The mean,
variance and expected exponential of the addition node are