

Next: Update Rules
Up: Cost Function
Previous: Terms of the Cost
This section describes how to compute the posterior mean and variance
of the outputs
fk(s(t)) of the MLP network. Ordinarily the
inputs, weights and biases of an MLP network have fixed values. Here
the inputs
s(t), weights
A,
B and the
biases
a,
b have posterior distributions which means
that we also have a posterior distribution of the outputs. One way to
evaluate the posterior mean and variance is to propagate distributions
instead of fixed values through the network. Whole distributions
would be quite tricky to deal with, and therefore we are going to
characterise the distributions by their mean and variance only.
The sources have mixture-of-Gaussians distributions for which it is
easy to compute the mean and variance:
Then the sources are multiplied with the first layer weight matrix
A and the bias
a is added. Let us denote the result
by
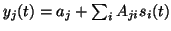 .
Since the sources, weights
and biases are all mutually independent a posteriori, the following
equations hold:
.
Since the sources, weights
and biases are all mutually independent a posteriori, the following
equations hold:
Equation (31) follows from the identity
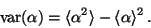 |
(23) |
For computing the posterior mean of the output
gj(yj(t)) of a
hidden neuron, we shall utilise the second order Taylor's series
expansion of gj around the posterior mean
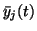 of its
input. This means that we approximate
of its
input. This means that we approximate
Since the posterior mean of yj(t) is by definition
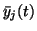 ,
the second term vanishes when evaluating the posterior mean, while the
posterior mean of
,
the second term vanishes when evaluating the posterior mean, while the
posterior mean of
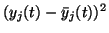 is by definition the
posterior variance
is by definition the
posterior variance
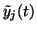 .
We thus have
.
We thus have
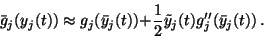 |
(25) |
The second order expansion was chosen because those are the terms
whose posterior mean can be expressed in terms of posterior mean and
variance of the input. Higher order terms would have required higher
order cumulants of the input, which would have increased the
computational complexity with little extra benefit.
For the posterior variance of
gj(yj(t)) the second order expansion
would result in terms which need higher than second order knowledge
about the inputs. Therefore we shall use the first order Taylor's
series expansion which then yields the following approximation for the
posterior variance of
gj(yj(t)):
![\begin{displaymath}\tilde{g}_j(y_j(t)) \approx [g'_j(\bar{y}_j(t))]^2 \tilde{y}_j(t) \, .
\end{displaymath}](img84.gif) |
(26) |
The next step is to compute the mean and variance of the output after
the second layer mapping. The outputs are given by
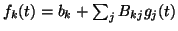 .
The equation for the posterior mean
.
The equation for the posterior mean
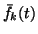 is similar to (30):
is similar to (30):
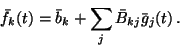 |
(27) |
The equation for the posterior variance
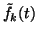 is more
complicated than (31), however, since si(t) are
independent a posterior but gj(t) are not. This is because each
si(t) affects several -- potentially all -- gj(t). In other
words, each si(t) affects each fk(t) through several paths which
interfere. This interference needs to be taken into account when
computing the posterior variance of fk(t).
is more
complicated than (31), however, since si(t) are
independent a posterior but gj(t) are not. This is because each
si(t) affects several -- potentially all -- gj(t). In other
words, each si(t) affects each fk(t) through several paths which
interfere. This interference needs to be taken into account when
computing the posterior variance of fk(t).
We shall use a first order approximation of the mapping
f(s(t)) for measuring the interference. This is
consistent with the first order approximation of the nonlinearities
gj and yields the following equation for the posterior variance of
fk(t):
where the posterior means of the partial derivatives are obtained by the
chain rule
and
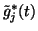 denotes the posterior variance of gj(t) without
the contribution from the sources. It can be computed as follows:
denotes the posterior variance of gj(t) without
the contribution from the sources. It can be computed as follows:
Notice that
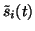 appears in (39) and
appears in (39) and
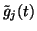 appears in (37). These terms do not
contribute to interference, however, because they are the parts which
are randomised by multiplication with Aji or Bkj and
randomising the phase destroys the interference, to use an analogy
from physics.
appears in (37). These terms do not
contribute to interference, however, because they are the parts which
are randomised by multiplication with Aji or Bkj and
randomising the phase destroys the interference, to use an analogy
from physics.


Next: Update Rules
Up: Cost Function
Previous: Terms of the Cost
Harri Lappalainen
2000-03-03