In the previous section we derived all the equations needed for the
computation of the cost function. Given the posterior means
![]() and variances
and variances
![]() and discrete
posterior probabilities
and discrete
posterior probabilities
![]() ,
we can compute the cost
function which measures the quality of the approximation of the
posterior pdf of the unknown variables. Any standard optimisation
algorithm could be used for minimising the cost function, but it is
sensible to utilise the particular form of the function. Due to lack
of space, we shall only outline the update rules but a more detailed
description can be found in [4].
,
we can compute the cost
function which measures the quality of the approximation of the
posterior pdf of the unknown variables. Any standard optimisation
algorithm could be used for minimising the cost function, but it is
sensible to utilise the particular form of the function. Due to lack
of space, we shall only outline the update rules but a more detailed
description can be found in [4].
Let us denote
C = Cq + Cp, where Cq is the part originating
from the expectation of
![]() and Cp is the part
originating from expectation of
and Cp is the part
originating from expectation of
![]() .
We shall
see how it is possible to derive efficient fixed point algorithms for
.
We shall
see how it is possible to derive efficient fixed point algorithms for
![]() and
and
![]() assuming that we have computed the
gradients of Cp with respect to the current estimates of
assuming that we have computed the
gradients of Cp with respect to the current estimates of
![]() and
and
![]() .
.
Since Cq has a term
![]() for each
for each
![]() whose posterior is approximated by Gaussian
whose posterior is approximated by Gaussian ![]() ,
solving for
,
solving for
![]() yields an update
rule for
yields an update
rule for
![]() :
:
| (33) |
| (34) |
| = | (35) | ||
| = | (36) |
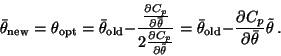 |
(37) |