Assuming the prior distribution of the parameters
![]() to be formed from Dirichlet distributions, makes the maximisation
step easy.
Let
to be formed from Dirichlet distributions, makes the maximisation
step easy.
Let
![]() ,
,
![]() be random variables such that
be random variables such that
![]() . In our case,
. In our case, ![]() are the transition
probabilities
are the transition
probabilities ![]() corresponding to a certain body or the
selection probabilities
corresponding to a certain body or the
selection probabilities ![]() corresponding to a certain type. A Dirichlet
distribution is defined as
corresponding to a certain type. A Dirichlet
distribution is defined as
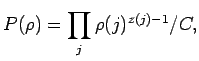 |
(10) |
The terms of log likelihood
![]() that depend on
that depend on
![]() can be written in the form
can be written in the form
![]() , where
, where
![]() are the expected counts of how many times
are the expected counts of how many times ![]() was used.
If we assume the counts
was used.
If we assume the counts ![]() to be constant and vary only the
probabilities
to be constant and vary only the
probabilities ![]() , we can find the maximum of the a posteriori
density analytically:
, we can find the maximum of the a posteriori
density analytically:
![$\displaystyle \rho(i)=\frac{s(i)+z(i)}{\sum_j \left[s(j)+z(j)\right]}$](img100.gif) |
(12) |