The ![]() and
and ![]() values computed by the forward-backward
algorithm are useful for many purposes. Firstly, the probability of
the observation sequence given the LOHMM is simply
values computed by the forward-backward
algorithm are useful for many purposes. Firstly, the probability of
the observation sequence given the LOHMM is simply
![]() . Secondly, the probability of
being in a state
. Secondly, the probability of
being in a state ![]() at time
at time ![]() given the observation sequence is
given the observation sequence is
![]() . Thirdly, computing the expected
counts required for the maximization step, becomes simple.
. Thirdly, computing the expected
counts required for the maximization step, becomes simple.
The forward-backward algorithm is based on dynamic programming. To
ease the computations, we find sets ![]() in the beginning of
learning. The set
in the beginning of
learning. The set ![]() is defined as the set of states at time
is defined as the set of states at time ![]() that are reachable from
start and are not conflicting with the
observation sequence
that are reachable from
start and are not conflicting with the
observation sequence
![]() . The reachable states can be
found in two phases:
. The reachable states can be
found in two phases:
Probabilities ![]() and
and ![]() are computed for each state in each
are computed for each state in each
![]() recursively. The
recursively. The
![]() is defined as the
probability of the partial observation sequence
is defined as the
probability of the partial observation sequence
![]() and state
and state ![]() at time
at time ![]() given the LOHMM. The
given the LOHMM. The
![]() is
the probability of the partial observation sequence
is
the probability of the partial observation sequence
![]() given state
given state ![]() at time
at time ![]() and the LOHMM. Set
and the LOHMM. Set
![]() and
and
![]() for every
for every
![]() . Recursion formulae are
. Recursion formulae are
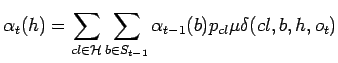 |
(6) | ||
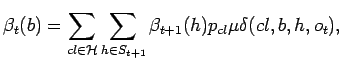 |
(7) |
The expected counts for the maximisation step are computed using
![]() and
and ![]() values. Let
values. Let
![]() be the probability
of going from state
be the probability
of going from state ![]() at time
at time ![]() to state
to state ![]() at time
at time ![]() using
the transition
using
the transition ![]() given the LOHMM and the observation sequence:
given the LOHMM and the observation sequence:
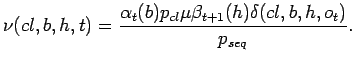 |
(8) |
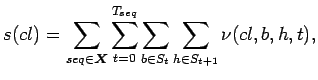 |
(9) |