


Next: Principal Component Analysis with
Up: Principal Component Analysis
Previous: Principal Component Analysis
works by applying gradient descent to the
reconstruction error (1) directly yielding the update
rules
Note that with
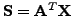 the update rule for
the update rule for
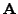 is a batch
version of Oja's subspace rule [7]. The algorithm finds a
basis in the subspace of the largest principal components. If needed,
the end result can be transformed into the PCA solution by proper
orthogonalization of
is a batch
version of Oja's subspace rule [7]. The algorithm finds a
basis in the subspace of the largest principal components. If needed,
the end result can be transformed into the PCA solution by proper
orthogonalization of
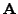 and
and
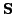 .
.
Tapani Raiko
2007-07-16