


Next: Subspace Learning Algorithm
Up: Principal Component Analysis for
Previous: Introduction
Assume that we have 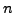
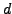 -dimensional data vectors
-dimensional data vectors
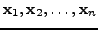 , which form the
, which form the 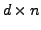 data matrix
data matrix
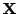 =
=
![$ [{\bf x}_1,{\bf x}_2,\ldots,{\bf x}_n]$](img8.png) . The matrix
. The matrix
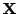 is
decomposed into
is
decomposed into
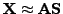 , where
, where
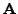 is a
is a 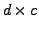 matrix,
matrix,
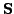 is a
is a 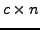 matrix and
matrix and
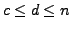 . Principal
subspace methods [6,4] find such
. Principal
subspace methods [6,4] find such
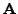 and
and
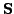 that the reconstruction error
that the reconstruction error
is minimized. Typically the row-wise mean is removed from
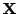 as a
preprocessing step. Without any further constraints, there exist
infinitely many ways to perform such a decomposition. PCA constraints
the solution by further requiring that the column vectors of
as a
preprocessing step. Without any further constraints, there exist
infinitely many ways to perform such a decomposition. PCA constraints
the solution by further requiring that the column vectors of
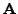 are
of unit norm and mutually orthogonal and the row vectors of
are
of unit norm and mutually orthogonal and the row vectors of
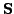 are
also mutually orthogonal
[3,4,2,5].
are
also mutually orthogonal
[3,4,2,5].
There are many ways to solve PCA
[6,4,2]. We will concentrate on the
subspace learning algorithm that can be easily adapted for the case of
missing values and further extended.
Subsections
Tapani Raiko
2007-07-16
![]()
![]() -dimensional data vectors
-dimensional data vectors
![]() , which form the
, which form the ![]() data matrix
data matrix
![]() =
=
![]() . The matrix
. The matrix
![]() is
decomposed into
is
decomposed into
![]() , where
, where
![]() is a
is a ![]() matrix,
matrix,
![]() is a
is a ![]() matrix and
matrix and
![]() . Principal
subspace methods [6,4] find such
. Principal
subspace methods [6,4] find such
![]() and
and
![]() that the reconstruction error
that the reconstruction error