Experiments with Image Data

HNFA+VM, presented in Chapter , was tested with a number of natural gray-scale images as a data set. Gaussian noise with standard deviation 0.1 was added to the images to avoid artefacts caused by the discrete gray levels from 0 to 255. The intensities were scaled to variance one.

10 times 10 image patches were taken randomly from the images to be used as data vectors. There was a total of 10000 data vectors. The data matrix X is thus 100 by 10000. The mean of each patch was subtracted from the patch and the data was whitened to a degree 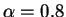$\alpha=0.8$ and rotated back to the original space:

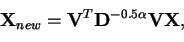$$\mathbf{X}_{new} = \mathbf{V}^T\mathbf{D}^{-0.5\alpha}\mathbf{V}\mathbf{X},$$ (8.1)

where V contains the orthonormal eigenvectors of the covariance matrix of the data and D is the diagonal matrix of its eigenvalues. Regular whitening corresponds to 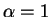$\alpha=1$ and whitening to a degree 0 would leave the data unchanged. The partly whitened version of the data was rotated back to the original space by multiplying with V^T from the left so that the dimensions of the data would still correspond to the pixels. Whitening is used, because the dominating feature of the images is the positive correlation between nearby pixels and the model could otherwise spend a layer just to model that. Regular whitening is typically used as a preprocessing for ICA.

Figure  shows the matrix V or the principal components of the data. There are only 99 components, since the removal of the mean in each image removes also one of the intrinsic dimensions. There is a great resemblance to the discrete cosine transform (DCT), which is widely used in image compression [21]. Compression and ensemble learning have much in common as was seen in Subsection . Taking into account that there are efficient algorithms for calculating the DCT, it is clearly a good choice for compression. None of the patches are localised in either PCA or DCT.

  

Figure: Left: The mixing matrix resulting from applying Principal Component Analysis (PCA) to the same data set. Right: the basis of the Discrete Cosine Transform (DCT) that is used in image compression.