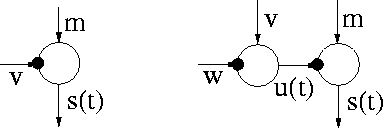Next: Formulation of the Model
Up: Hierarchical Nonlinear Factor Analysis
Previous: Hierarchical Nonlinear Factor Analysis
In most currently used models, the means of Gaussian nodes have
hierarchical or dynamical models. In many real cases the variance is
not constant either but it is more difficult to model it (see Section
![[*]](cross_ref_motif.gif) ). A variance neuron shown in
Figure
). A variance neuron shown in
Figure ![[*]](cross_ref_motif.gif) is designed for that. It can convert a
prediction of mean into a prediction of variance and thus allows to
build hierarchical or dynamical models for the variance. In general,
the variance neuron results in a heavy-tailed super-Gaussian model for
the Gaussian node it is attached to as described in
Section
is designed for that. It can convert a
prediction of mean into a prediction of variance and thus allows to
build hierarchical or dynamical models for the variance. In general,
the variance neuron results in a heavy-tailed super-Gaussian model for
the Gaussian node it is attached to as described in
Section ![[*]](cross_ref_motif.gif) . This can be useful for instance in modelling
outliers in the observations.
. This can be useful for instance in modelling
outliers in the observations.
Figure 5.1:
Left: Source s(t) has a time independent prior variance v.
Right: A variance neuron is included to give a time dependent
prior variance u(t) for the source s(t).
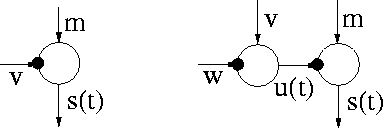 |
In many cases, the amount of noise depends on the amplitude of a signal.
To model that, one would like to
connect the same variable to both the mean and variance priors of a
neuron. Unfortunately, this is not allowed because of the fourth
restriction concerning the independence assumptions. Instead, one can
attach the variable to the mean inputs of a neuron s(t) and its
variance neuron u(t). This effectively results in a correlation
between the mean and the variance of s(t). The addition of the
variance neuron in between restores the formal independency at the
expense of increased cost.




Next: Formulation of the Model
Up: Hierarchical Nonlinear Factor Analysis
Previous: Hierarchical Nonlinear Factor Analysis
Tapani Raiko
2001-12-10
![[*]](cross_ref_motif.gif) ). A variance neuron shown in
Figure
). A variance neuron shown in
Figure ![[*]](cross_ref_motif.gif) is designed for that. It can convert a
prediction of mean into a prediction of variance and thus allows to
build hierarchical or dynamical models for the variance. In general,
the variance neuron results in a heavy-tailed super-Gaussian model for
the Gaussian node it is attached to as described in
Section
is designed for that. It can convert a
prediction of mean into a prediction of variance and thus allows to
build hierarchical or dynamical models for the variance. In general,
the variance neuron results in a heavy-tailed super-Gaussian model for
the Gaussian node it is attached to as described in
Section ![[*]](cross_ref_motif.gif) . This can be useful for instance in modelling
outliers in the observations.
. This can be useful for instance in modelling
outliers in the observations.