Variance model of image sequences

In this section an experiment with a dynamical model for variances applied to image sequence analysis is reported. The motivation behind modelling variances is that in many natural signals, there exists higher order dependencies which are well characterised by correlated variances of the signals Parra00NIPS. Hence we postulate that we should be able to better catch the dynamics of a video sequence by modelling the variances of the features instead of the features themselves. This indeed is the case as will be shown.

The model considered can be summarised by the following set of equations:

$${\mathbf{x}}(t) \sim \mathcal N({\mathbf{A}} {\mathbf{s}}(t), \operatorname{diag}(\exp[-{\mathbf{v}}_x]))$$

$${\mathbf{s}}(t) \sim \mathcal N({\mathbf{s}}(t-1), \operatorname{diag}(\exp[-{\mathbf{u}}(t)]))$$

$${\mathbf{u}}(t) \sim \mathcal N({\mathbf{B}} {\mathbf{u}}(t-1), \operatorname{diag}(\exp[-{\mathbf{v}}_u]))$$

We will use the acronym DynVar in referring to this model. The linear mapping ${\mathbf{A}}$ from sources ${\mathbf{s}}(t)$ to observations ${\mathbf{x}}(t)$ is constrained to be sparse by assigning each source a circular region on the image patch outside of which no connections are allowed. These regions are still highly overlapping. The variances ${\mathbf{u}}(t)$ of the innovation process of the sources have a linear dynamical model. It should be noted that modelling the variances of the sources in this manner is impossible if one is restricted to use conjugate priors.

The sparsity of $\bf {A}$ is crucial as the computational complexity of the learning algorithm depends on the number of connections from ${\bf s}(t)$ to ${\bf x}(t)$. The same goal could have been reached with a different kind of approach as well. Instead of constraining the mapping to be sparse from the very beginning of learning it could have been allowed to be full for a number of iterations and only after that pruned based on the cost function as explained in Section 6.2. But as the basis for image sequences tends to get sparse anyway, it is a waste of computational resources to wait while most of the weights in the linear mapping tend to zero.

For comparison purposes, we postulate another model where the dynamical relations are sought directly between the sources leading to the following model equations:

$${\mathbf{x}}(t) \sim \mathcal N({\mathbf{A}} {\mathbf{s}}(t), \operatorname{diag}(\exp[-{\mathbf{v}}_x]))$$

$${\mathbf{s}}(t) \sim \mathcal N({\mathbf{B}} {\mathbf{s}}(t-1), \operatorname{diag}(\exp[-{\mathbf{u}}(t)]))$$

We shall refer to this model as DynSrc.

The data ${\mathbf{x}}(t)$ was a video image sequence Hateren98 of dimensions $16 \times 16 \times 4000$. That is, the data consisted of 4000 subsequent digital images of the size $16 \times 16$. A part of the data set is shown in Figure 14.

Figure 14: A sequence of 80 frames from the data used in the experiment.

[width=0.5]Vid12

Both models were learned by iterating the learning algorithm 2000 times at which stage a sufficient convergence was attained. The first hint of the superiority of the DynVar model was provided by the difference of the cost between the models which was 28 bits/frame [for the coding interpretation, see][]Honkela04TNN. To further evaluate the performance of the models, we considered a simple prediction task where the next frame was predicted based on the previous ones. The predictive distributions, $p({\mathbf{x}}(t+1)\vert{\mathbf{x}}(1),...,{\mathbf{x}}(t))$, for the models can be approximately computed based on the posterior approximation. The means of the predictive distributions are very similar for both of the models. Figure 15 shows the means of the DynVar model for the same sequence as in Figure 14. The means themselves are not very interesting, since they mainly reflect the situation in the previous frame. However, the DynVar model provides also a rich model for the variances. The standard deviations of its predictive distribution are shown in Figure 16. White stands for a large variance and black for a small one. Clearly, the model is able to increase the predicted variance in the area of high motion activity and hence provide better predictions. We can offer quantitative support for this claim by computing the predictive perplexities for the models. Predictive perplexity is widely used in language modelling and it is defined as

$$\mathrm{perplexity}(t)=\exp\left\{-\frac{1}{256}\sum_{i=1}^{256} \log p(x_i(t+1)\vert{\mathbf{x}}(1),...,{\mathbf{x}}(t)) \right\}.$$

The predictive perplexities for the same sequence as in Figure 14 are shown in Figure 17. Naturally the predictions get worse when there is movement in the video. However, DynVar model is able to handle it much better than the compared DynSrc model. The same difference can also be directly read by comparing the cost functions (3).

Figure 15: The means of the predictive distribution for the DynVar model.

[width=0.5]VarPredMean

Figure 16: The standard deviations of the predictive distribution for the DynVar model.

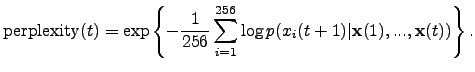[width=0.5]VarPredVar

Figure 17: Predictive perplexities.

[width=0.6]PredPerp

The possible applications for a model of image sequences include video compression, motion detection, early stages of computer vision, and making hypotheses on biological vision.