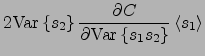Structural learning and local minima

The chosen model has a pre-specified structure which, however, has some flexibility. The number of nodes is not fixed in advance, but their optimal number is estimated using variational Bayesian learning, and unnecessary connections can be pruned away.

A factorial posterior approximation, which is used in this paper, often leads to automatic pruning of some of the connections in the model. When there is not enough data to estimate all the parameters, some directions remain ill-determined. This causes the posterior distribution along those directions to be roughly equal to the prior distribution. In variational Bayesian learning with a factorial posterior approximation, the ill-determined directions tend to get aligned with the axes of the parameter space because then the factorial approximation is most accurate.

The pruning tendency makes it easy to use for instance sparsely connected models, because the learning algorithm automatically selects a small amount of well-determined parameters. But at the early stages of learning, pruning can be harmful, because large parts of the model can get pruned away before a sensible representation has been found. This corresponds to the situation where the learning scheme ends up into a local minimum of the cost function MacKay01. A posterior approximation which takes into account the posterior dependences has the advantage that it has far less local minima than a factorial posterior approximation. It seems that Bayesian learning algorithms which have linear time complexity cannot avoid local minima in general.

However, suitable choices of the model structure and countermeasures included in the learning scheme can alleviate the problem greatly. We have used the following means for avoiding getting stuck into local minima:

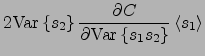• Learning takes place in several stages, starting from simpler structures which are learned first before proceeding to more complicated hierarchic structures. An example of this technique was presented in Section 5.3.
• New parts of the network are initialised appropriately. One can use for instance principal component analysis (PCA), independent component analysis (ICA), vector quantisation, or kernel PCA Honkela04ICA. The best option depends on the application. Often it is useful to try different methods and select the one providing the smallest value of the cost function for the learned model. There are two ways to handle initialisation: either to fix the sources for a while and learn the weights of the model, or to fix the weights for a while and learn the sources corresponding to the observations. The fixed variables can be released gradually (see Section 5.1 of Valpola03ICA_Nonlin).
• Automatic pruning is discouraged initially by omitting the term

  $$2 \mathrm{Var}\left\{s_2\right\} \frac{\partial C}{\partial \mathrm{Var}\left\{s_1 s_2\right\}} \left< s_1 \right>$$

  
  
  in the multiplication nodes (Eq. (28)). This effectively means that the mean of $s_1$ is optimistically adjusted as if there were no uncertainty about $s_2$. In this way the cost function may increase at first due to overoptimism, but it may pay off later on by escaping early pruning.
• New sources $s_i(t)$ (components of the source vector ${\bf s}(t)$ of a layer) are generated, and pruned sources are removed from time to time.
• The activations of the sources are reset a few times. The sources are re-adjusted to their places while keeping the mapping and other parameters fixed. This often helps if some of the sources are stuck into a local minimum.