(MDS) refers to a group of methods that is widely used especially in behavioral, econometric, and social sciences to analyze subjective evaluations of pairwise similarities of entities, such as commercial products in a market survey. The starting point of MDS is a matrix consisting of the pairwise dissimilarities of the entities. In this thesis only distances between pattern vectors in a Euclidean space will be considered, but in MDS the dissimilarities need not be distances in the mathematically strict sense. In fact, MDS is perhaps most often used for creating a space where the entities can be represented as vectors, based on some evaluation of the dissimilarities of the entities.
The goal in this thesis is not merely to create a space which would represent the relations of the data faithfully, but also to reduce the dimensionality of the data set to a sufficiently small value to allow visual inspection of the set. The MDS methods can be used to fulfill this goal, as well.
There exists a multitude of variants of MDS with slightly different cost functions and optimization algorithms. The first MDS for metric data was developed in the 1930s (historical treatments and introductions to MDS have been provided by, for example, Kruskal and Wish, 1978; de Leeuw and Heiser, 1982; Wish and Carroll, 1982; Young, 1985), and later generalized for analyzing nonmetric data and even the common structure in several dissimilarity matrices corresponding to, for instance, evaluations made by different individuals.
The algorithms designed for analyzing a single dissimilarity matrix, and which can thus be used for reducing the dimensionality of a data set, can be broadly divided into two basic types, metric and nonmetric MDS.
In the original metric MDS (Torgerson, 1952; cf. Young and
Householder, 1938) the distances between
the data items have been given, and a configuration of points that
would give rise to the distances is sought. Often a linear projection
onto a subspace obtained with PCA is used. The key idea of the
method, to approximate the original set of distances with distances
corresponding to a configuration of points in a Euclidean space can,
however, also be used for constructing a nonlinear projection method.
If each item ![]() is represented with a lower-dimensional, say,
two-dimensional data vector
is represented with a lower-dimensional, say,
two-dimensional data vector ![]() , then the goal of the
projection is to optimize the representations so that the distances
between the items in the two-dimensional space will be as close to the
original distances as possible. If the distance between
, then the goal of the
projection is to optimize the representations so that the distances
between the items in the two-dimensional space will be as close to the
original distances as possible. If the distance between ![]() and
and ![]() is denoted by d(k,l) and the distance between
is denoted by d(k,l) and the distance between ![]() and
and ![]() in the two-dimensional space by d'(k,l),
the metric MDS tries to approximate d(k,l) by d'(k,l). If a
square-error cost is used, the objective function to be minimized can
be written as
in the two-dimensional space by d'(k,l),
the metric MDS tries to approximate d(k,l) by d'(k,l). If a
square-error cost is used, the objective function to be minimized can
be written as
A perfect reproduction of the Euclidean distances may not always be the best possible goal, especially if the components of the data vectors are expressed on an ordinal scale. Then only the rank order of the distances between the vectors is meaningful, not the exact values. The projection should try to match the rank order of the distances in the two-dimensional output space to the rank order in the original space. The best possible rank ordering for a given configuration or points can be guaranteed by introducing a monotonically increasing function f that acts on the original distances, and always maps the distances to such values that best preserve the rank order. Nonmetric MDS [Kruskal, 1964, Shepard, 1962] uses such a function [Kruskal and Wish, 1978], whereby the normalized cost function becomes
For any given configuration of the projected points
![]() , f is always chosen to minimize Equation 3.
, f is always chosen to minimize Equation 3.
Although the nonmetric MDS was motivated by the need of treating ordinal-scale data, it can also be used of course if the inputs are presented as pattern vectors in a Euclidean space. The projection then only tries to preserve the order of the distances between the data vectors, not their absolute values. A demonstration of nonmetric MDS, applied in a dimension reduction task, is given in Figure 3.

Figure: A nonlinear projection constructed using nonmetric MDS. The
data set is the same as in Figure 2. Missing
data values were treated by the following simple method, which has
been demonstrated to produce good results at least in the pattern
recognition context [Dixon, 1979]. When computing the
distance between a pair of data items, only the (squared) differences
between component values that are available are computed. The rest
of the differences are then set to the
average of the computed differences.
Another nonlinear projection method, Sammon's mapping [Sammon, Jr., 1969], is closely related to the metric MDS version described above. It, too, tries to optimize a cost function that describes how well the pairwise distances in a data set are preserved. The cost function of Sammon's mapping is (omitting a constant normalizing factor)
The only difference between Sammon's mapping and the (nonlinear) metric MDS (Eq. 2) is that the errors in distance preservation are normalized with the distance in the original space. Because of the normalization the preservation of small distances will be emphasized.
A demonstration of Sammon's mapping is presented in Figure 4.
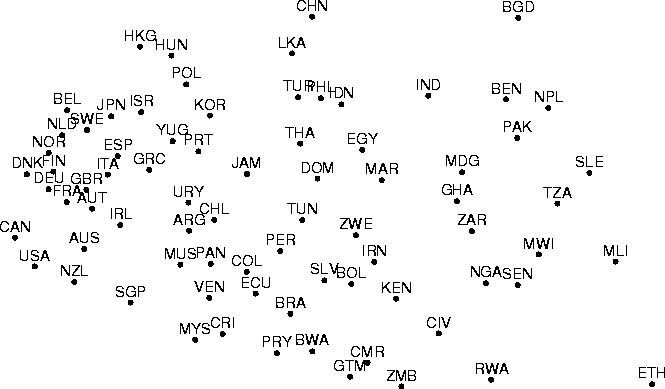
Figure: Sammon's mapping of the data set which has been projected
using PCA in Figure 2 and nonmetric MDS in
Figure 3. Missing data values were treated
in the same manner as in forming the nonmetric MDS.