One can use the SVD approach (4) in order to find an
approximate solution to the PCA problem. However, estimating the
covariance matrix
![]() becomes very difficult when there are lots of
missing values. If we estimate
becomes very difficult when there are lots of
missing values. If we estimate
![]() leaving out terms with missing
values from the average, we get for the estimate of the covariance matrix
leaving out terms with missing
values from the average, we get for the estimate of the covariance matrix
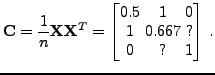 |
(9) |
Another option is to complete the data matrix by iteratively imputing
the missing values (see, e.g., [2]). Initially, the
missing values can be replaced by zeroes. The covariance matrix of the
complete data can be estimated without the problems mentioned
above. Now, the product
![]() can be used as a better estimate for
the missing values, and this process can be iterated until
convergence. This approach requires the use of the complete data
matrix, and therefore it is computationally very expensive if a large
part of the data matrix is missing. The time complexity of computing
the sample covariance matrix explicitly is
can be used as a better estimate for
the missing values, and this process can be iterated until
convergence. This approach requires the use of the complete data
matrix, and therefore it is computationally very expensive if a large
part of the data matrix is missing. The time complexity of computing
the sample covariance matrix explicitly is ![]() .
We will further refer to this approach as the imputation algorithm.
.
We will further refer to this approach as the imputation algorithm.
Note that after convergence, the missing values do not contribute to the reconstruction error (2). This means that the imputation algorithm leads to the solution which minimizes the reconstruction error of observed values only.