


Next: EM Algorithm
Up: Algorithms for Principal Component
Previous: Principal subspace and components
PCA can be determined by using the singular value decomposition (SVD) [5]
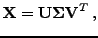 |
(3) |
where
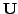 is a
is a 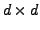 orthogonal matrix,
orthogonal matrix,
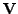 is an
is an 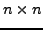 orthogonal matrix and
orthogonal matrix and
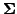 is a
is a 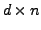 pseudodiagonal matrix (diagonal
if
pseudodiagonal matrix (diagonal
if 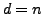 ) with the singular values on the main diagonal [5].
The PCA solution is obtained by selecting the
) with the singular values on the main diagonal [5].
The PCA solution is obtained by selecting the 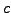 largest singular values
from
largest singular values
from
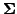 , by forming
, by forming
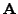 from the corresponding
from the corresponding 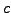 columns of
columns of
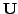 ,
and
,
and
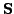 from the corresponding
from the corresponding 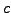 rows of
rows of
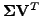 .
.
Note that PCA can equivalently be defined using the eigendecomposition
of the 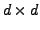 covariance matrix
covariance matrix
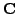 of the column vectors of
the data matrix
of the column vectors of
the data matrix
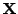 :
:
Here, the diagonal matrix
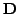 contains the eigenvalues of
contains the eigenvalues of
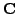 ,
and the columns of the matrix
,
and the columns of the matrix
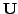 contain the unit-length eigenvectors of
contain the unit-length eigenvectors of
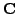 in the same order [6,4,2,5].
Again, the columns of
in the same order [6,4,2,5].
Again, the columns of
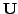 corresponding to the largest eigenvalues are
taken as
corresponding to the largest eigenvalues are
taken as
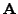 , and
, and
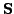 is computed as
is computed as
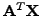 . This approach can be
more efficient for cases where
. This approach can be
more efficient for cases where 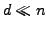 , since it avoids the
, since it avoids the 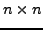 matrix.
matrix.



Next: EM Algorithm
Up: Algorithms for Principal Component
Previous: Principal subspace and components
Tapani Raiko
2007-09-11
![]() covariance matrix
covariance matrix
![]() of the column vectors of
the data matrix
of the column vectors of
the data matrix
![]() :
: