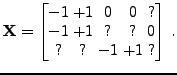Next: Adapting SVD
Up: Principal Component Analysis for
Previous: Subspace Learning Algorithm
Let us consider the same problem when the data matrix has missing
entries![[*]](file:/usr/share/latex2html/icons/footnote.png) . In the following there are
. In the following there are 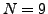 observed values
and
observed values
and 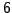 missing values marked with a question mark (?):
missing values marked with a question mark (?):
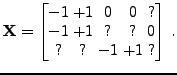 |
(8) |
We would like to find
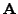 and
and
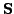 such
that
such
that
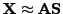 for the observed data values. The rest of
the product
for the observed data values. The rest of
the product
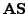 represents the reconstruction of missing values.
represents the reconstruction of missing values.
Subsections
Tapani Raiko
2007-09-11
![]() . In the following there are
. In the following there are ![]() observed values
and
observed values
and ![]() missing values marked with a question mark (?):
missing values marked with a question mark (?):