In nonlinear relational Markov networks (NRMN), the clique potentials
are replaced by a probability density function for continuous
values, in this case HNFA![]() The combination of these two methods is not completely
straightforward. For instance, marginalisation required by the BP
algorithm is often difficult with nonlinear models. Also, algorithmic
complexity needs to be considered, since the model will be quite
demanding. One of the key points is to use probability densities
The combination of these two methods is not completely
straightforward. For instance, marginalisation required by the BP
algorithm is often difficult with nonlinear models. Also, algorithmic
complexity needs to be considered, since the model will be quite
demanding. One of the key points is to use probability densities ![]() in place of potentials
in place of potentials
![]() . Then, overlapping templates give
multiple probability functions for some variable and they are
combined using the product-of-experts combination rule described below.
. Then, overlapping templates give
multiple probability functions for some variable and they are
combined using the product-of-experts combination rule described below.
Combination Rules: One of the non-trivialities in making relational extensions of probabilistic models is the so called combination rule [7]. When the structure of the graphical model is determined by the data, one cannot know in advance how many links there are for each node. One solution is to use combination rules such as the noisy-or. Combination rule transforms a number of probability functions into one. Noisy-or does not generalise well to continuous values, but two alternatives are introduced below.
Using a Markov network and the BP algorithm corresponds to using
probability densities as potentials and the maximum entropy
combination rule. The probability densities
![]() are combined
to form the joint probability distribution by maximising the entropy
of
are combined
to form the joint probability distribution by maximising the entropy
of
![]() given that all instantiations of
given that all instantiations of
![]() coalesce
with the corresponding marginals of
coalesce
with the corresponding marginals of
![]() . For singly connected
networks, this means that the joint distribution is
. For singly connected
networks, this means that the joint distribution is
![]() , where
, where ![]() runs over pairs of
instantiations of templates and
runs over pairs of
instantiations of templates and
![]() contains the shared
attributes in those pairs.
Marginalisation of nonlinear models cannot usually be done exactly and
therefore one should be very careful with the denominator. Also,
one should take care in handling loops.
contains the shared
attributes in those pairs.
Marginalisation of nonlinear models cannot usually be done exactly and
therefore one should be very careful with the denominator. Also,
one should take care in handling loops.
In the product-of-experts (PoE) combination rule, the logarithm of the
probability density of each variable is the average of the logarithms
of the probability functions that the variable is included in:
![]() for all
for all
![]() , where only those
, where only those ![]() instantiated templates
instantiated templates ![]() that contain
that contain ![]() , are considered. PoE is easy to implement in the
variational Bayesian framework because
the term in the cost function
(3) can be split into familiar looking terms.
Consider the combination of two probability functions
, are considered. PoE is easy to implement in the
variational Bayesian framework because
the term in the cost function
(3) can be split into familiar looking terms.
Consider the combination of two probability functions
![]() and
and ![]() (that are assumed to be independent):
(that are assumed to be independent):
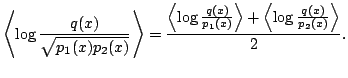 |
(4) |
Inference in Loopy Networks:
Inferring unobserved attributes in a database is in this case an iterative process
which should end up in a cohesive whole. Information can traverse
through multiple relations.
![]() The basic element in the inference algorithm of Bayes Blocks is the
update of the posterior approximation
The basic element in the inference algorithm of Bayes Blocks is the
update of the posterior approximation ![]() of a single unknown
variable, assuming the rest of the distribution fixed. The update is
done such that the cost function (3) is minimised. One
should note that when the distribution over the Markov blanket of a
variable is fixed, the local update rules apply, regardless of any
loops in the network. Therefore the use of local update rules is well
founded, that is, local inference in a loopy network does not bring
any additional heuristicity to the system. Also, since the inference
is based on minimising a cost function, the convergence is guaranteed,
unlike in the BP algorithm.
of a single unknown
variable, assuming the rest of the distribution fixed. The update is
done such that the cost function (3) is minimised. One
should note that when the distribution over the Markov blanket of a
variable is fixed, the local update rules apply, regardless of any
loops in the network. Therefore the use of local update rules is well
founded, that is, local inference in a loopy network does not bring
any additional heuristicity to the system. Also, since the inference
is based on minimising a cost function, the convergence is guaranteed,
unlike in the BP algorithm.
Learning:
The learning or parameter estimation problem is to find the
probability functions associated with the given clique templates
![]() . Now that we use probability functions instead of
potentials, it is possible in some cases to separate the
learning problem into parts. For each template
. Now that we use probability functions instead of
potentials, it is possible in some cases to separate the
learning problem into parts. For each template
![]() , find
the appropriate instantiations
, find
the appropriate instantiations
![]() and collect the associated
attributes
and collect the associated
attributes
![]() into a table. Learn a HNFA model for this table
ignoring the underlying relations.
This divide-and-conquer strategy makes learning comparatively fast,
because all the interaction is avoided. There are some cases that
forbid this. If the data contains missing values, they need
to be inferred using the method in the previous paragraph. Also, it is
possible to train experts cooperatively rather than separately
[3].
into a table. Learn a HNFA model for this table
ignoring the underlying relations.
This divide-and-conquer strategy makes learning comparatively fast,
because all the interaction is avoided. There are some cases that
forbid this. If the data contains missing values, they need
to be inferred using the method in the previous paragraph. Also, it is
possible to train experts cooperatively rather than separately
[3].
Clique Templates:
In data mining, so called frequent sets are often mined from binary
data. Frequent sets are groups of binary variables that get the value ![]() together often enough to be called frequent. The generalisation of
this concept to continuous values could be called the interesting
sets. An interesting set contains variables that have such strong
mutual dependencies that the whole is considered interesting. The
methodology of inductive logic programming could be applied to finding
interesting clique templates. The definition of a measure for
interestingness is left as future work.
Note that the divide-and-conquer strategy described in the previous
paragraph becomes even more important if one needs to consider
different sets of templates. One can either learn a model for
each template separately and then try combinations with the
learned models, or try a combination of templates and learn
cooperatively the models for them. Naturally the number of
templates is much smaller than the number of combinations and thus the
first option is computationally much cheaper.
together often enough to be called frequent. The generalisation of
this concept to continuous values could be called the interesting
sets. An interesting set contains variables that have such strong
mutual dependencies that the whole is considered interesting. The
methodology of inductive logic programming could be applied to finding
interesting clique templates. The definition of a measure for
interestingness is left as future work.
Note that the divide-and-conquer strategy described in the previous
paragraph becomes even more important if one needs to consider
different sets of templates. One can either learn a model for
each template separately and then try combinations with the
learned models, or try a combination of templates and learn
cooperatively the models for them. Naturally the number of
templates is much smaller than the number of combinations and thus the
first option is computationally much cheaper.
So what are meaningful candidates for clique templates? For instance,
the template
![]() does not make much
sense. Variables
does not make much
sense. Variables ![]() and
and ![]() are not related to each other, so when
all pairs are considered,
are not related to each other, so when
all pairs are considered,
![]() and
and
![]() are always independent and thus uninteresting by definition. In
general, a template is uninteresting, if it can be split into two
parts that do not share any variables.
When considering large templates, the number of involved attributes
grows large as well, which makes learning more involved. An
interesting possibility is to make a hierarchical model.
When a
large template contains others as subtemplates, one can use the
factors
are always independent and thus uninteresting by definition. In
general, a template is uninteresting, if it can be split into two
parts that do not share any variables.
When considering large templates, the number of involved attributes
grows large as well, which makes learning more involved. An
interesting possibility is to make a hierarchical model.
When a
large template contains others as subtemplates, one can use the
factors
![]() in Eq. (1, 2) of the
subtemplate as the attributes for the large template. The factors
already capture the internal structure of the subtemplates and
thus the probabilistic model of the large template needs only to
concentrate on the structure between its subtemplates.
in Eq. (1, 2) of the
subtemplate as the attributes for the large template. The factors
already capture the internal structure of the subtemplates and
thus the probabilistic model of the large template needs only to
concentrate on the structure between its subtemplates.