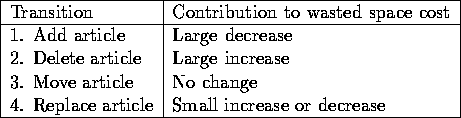
In the second experiment, the motivation was to solve the problem of fax newspaper better than in the first experiment. The problem of the previous approach was that finding a good layout might take several annealing rounds, and this was considered far too slow for the fax newspaper application considered. Thus it was deemed essential to perform some of the selection of material also within the algorithm building the layout. The ensuing increase in problem size had to be countered by redefining the problem formulation, especially the state space. To counter the increase in problem size and to ensure that overlaps would not occur in the resulting layouts, overlapping during annealing was not allowed at all.
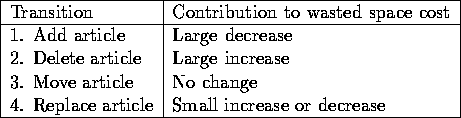
The transitions move and replace are actually combinations of add and delete. The problem with move is that although it does contribute to the value of the page layout in the long term, no cost change can easily be associated with the change when minimizing only empty space or maximizing priority value of material on a page. All moves would then have zero effect on the cost and would therefore be accepted at any time of the annealing, and the system could for a long time alternate between two equivalent states. In fact, this happened with the previous experiment, SA1.
Delete was also considered problematic, because it introduces such a large addition to the page cost states, and actually is just a leading step in an actual change. This means that if transitions delete and add are used, the actually interesting transitions necessarily have a high mountain peak to climb over on the delete transition. Therefore, at lower temperatures no deletions would be accepted. This dilemma led to consideration of the transition replace, and the following idea emerged: add was combined with replace to produce the transition replace if overlap, which works as follows:
In each transition, one article is added to the page and zero or more articles are removed. See Fig. 13 for an example of a transition where a replace occurs due to a collision.
Figure: A replace-if-overlap transition during the
annealing for a 5-column page, with snapshots of the page before and
after the transition. The shaded boxes are articles, the shades of
gray showing the priority values (dark has high priority). The thick
black lines stand for gaps, i.e. contiguous empty spaces where
articles could be added. On the left is the situation before an
accepted transition. On the right side is the same page after adding
article 31 into the upper left corner of an empty region. The addition
resulted in an overlap with article 22, which was therefore thrown
out.
In the selection of the suggested position, the VIP empty regions -mechanism was used (see Fig. 14). In the region formulation, the empty space on a page is represented as a group of rectangular, potentially overlapping regions, defined by the borders of existing articles on the page. Each region is maximal, i.e. it could not be extended horizontally or vertically. All empty space on the page is covered by at least one region.
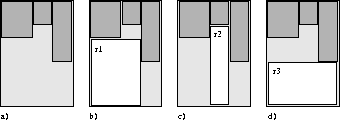
Figure: a) A sample page layout in the middle of pagination, with
three articles placed. b), c) and d) The three maximal empty regions,
r1, r2 and r3 that can be found from the layout.
In the average about 1500 rounds (i.e. suggested moves) were used in annealing, with a final period of 30 rounds in zero temperature to further ensure being in the bottom of a minimum.
Since the goal was to maximize the amount of high-priority material on the page and minimize empty space, both of these factors were used in the cost function. The energy of a whole page was therefore calculated with the following equation:
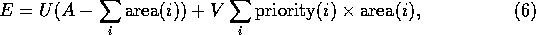
where i denotes an article, A is the total available space on page, and U and V are weights used to set the balance between minimizing empty space and maximizing priority value, respectively. The first term of the sum calculates the empty space on a page, the second producing the priority value of the page, 1 being the best priority and 10 the worst. Thus also the second term must be minimized to maximize the actual value of the page. Therefore, the energy change pertaining to a single transition is given by
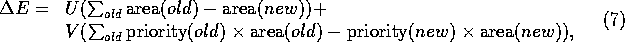
where old and new denote the outgoing and incoming articles, respectively. Since minimization of empty space was considered important, it was weighted relatively high in the cost function.
As mentioned before, the layout problem is NP-complete. To gain a more exact idea about the problem complexity, some analysis of the size of the state space was carried out.
The calculation of the number of possible article combinations on the page may be divided into two parts: selection of articles for the page, and selection of the exact version, article form, for each article on the page. For the sake of simplicity it may be assumed that each article has the same amount of versions. Thus the number of possible combinations for a fixed number of articles on the page is:
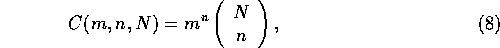
where m stands for the number of article versions per article, n is the number of articles selected on the page and N is the total number of articles to choose from. Since the number of articles on the page may vary depending on the available material, the total number of combinations is given by summing the counts produced by each number of articles that may reside on the page, and the equation thus becomes
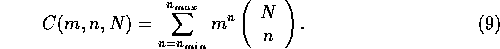
As noted before, this describes only the number of different possible article combinations. The total number of states would be the number of article combinations times the number of possible layouts per combination. Calculating all the different possible layouts that an article combination produces is practically impossible, as it depends heavily on the available data. In addition, most the available state space may actually never be traversed, and it is virtually impossible to find out the actual probability distribution of visiting different areas of the state space. This analysis of the size of the state space was nevertheless provided, since it may be illuminating in comparison with the approach of SA1.
The implementation was tested with the same material as in the previous two experiments. Fig. 15 depicts a full page obtained in one run of the algorithm, a result of quality which never occurred when experimenting with the SA1 or VIPÊ methods with the same material.

Figure: A good result especially in terms of wasted space.
The results obtained with SA2 were compared to those obtained with pure gradient-descent algorithm. Pure gradient-descent equals to running SA with temperature zero, i.e. accepting only transitions leading downward. As may be seen from Fig. 16, even applying gradient-descent in this problem formulation produces results that are not completely unacceptable. However, SA on the right of Fig. 16 performs clearly better. This comparison suggests that while SA performs very well with these few goals, after adding goals it still would perform rather well, whereas gradient-descent would probably do poorly.
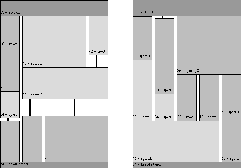
Figure: Two sample layouts produced out of the same material a)
with pure gradient-descent and b) with SA.