The theory of SA leaves plenty of implementation details unspecified, since due to time constraints SA can never be applied in the form for which the theory guarantees optimal behavior. The numerous experiments with SA have however produced useful implementation knowledge. Hints exist for choosing several control parameters affecting the algorithm [Aarts and Korst, 1989]. Still, some of these hints are rather arbitrary, as are the guidelines on how to choose the state space and the allowed transitions. Success in formulating the problem to best suit to SA requires some experience and understanding of the algorithm.
The following problem formulation is a final stage in a series of
tests with slightly different state spaces and transitions as well as
values for the control parameters. The two tasks of
pagination---selection of material and creation of the layout---were
separated in this approach. First, it was attempted to select "good"
initial material consisting of boxes with fixed size, shape and
contents (such as advertisements or editorial articles already laid
out to some shape) and then annealing was used to find a layout where
these boxes would not overlap. Naturally, in this scheme a solution
may not be even reachable with the selected boxes. Regardless, this
choice was made in order to reduce the state space for annealing,
since the annealing approach selected turned out to be so
slow
.
The first task was to select those article forms that would participate in the annealing of the page
layout. A simple but effective scheme was needed for generation and
selection of suitable article combinations, since it definitely was
not desirable to go through the time-consuming annealing process with
article combinations that were known to be unfitting or otherwise
poor. A generate-and-test approach was needed. That is, we
wanted to
For the generation of prospective solutions, a method following the metaphor of an adder for numbers with variable base was devised. Within this metaphor, each combination of digits (i.e. a number like 5366) represented one combination of article versions (version 5 of article 1, version 3 of article 2, version 6 of articles 3 and 4).
A binary number system could therefore represent articles where each has two versions. The decimal number system accordingly would represent articles with ten different versions each. However, since the available articles had different number of versions (minimun two, with one actual version and the other meaning that the article was not included on the page at all), the base of the system needed to vary according to the number of versions that each article had, i.e. the base was individual for each digit position. See Table 2 for an example. By going through each number representable with this number system, all the possible article version combinations are produced. This may be carried out by starting with number zero and incrementing it one at a time. Therefore, this generation method was called a variable-base adder.
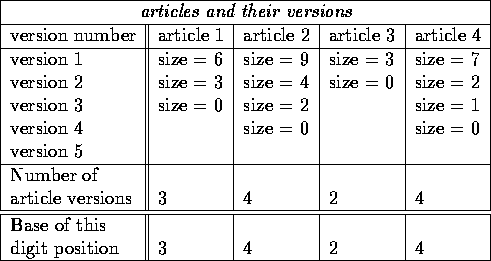
Table: Four articles with varying number of versions and
their correspondence to a number system with individually defined base
for each digit position. Each article is represented in one digit
position. The base in this position is the number of versions the
article has. The versions of the article correspond to digits from
zero to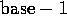 
. In this table, a version is characterized by its
size. Zero size means that the article does not appear on the page at
all.
The best-first order of prospective solutions was achieved by assigning the articles to digit positions in the order of their priority, and arranging the article versions in the order of size from large to small. This ordering tends to maximize the amount of any higher prority material on page before descending to material of lower priorities, and produces an order roughly from best to worst in terms of the total priority of the material on the page, when the priority of a page is defined as follows:
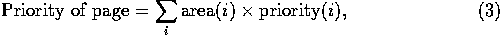
where i goes through the article versions on the page.
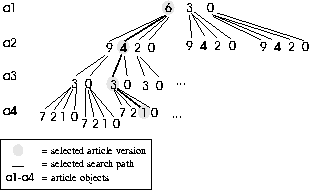
Figure: A search tree representing the order in which the
solutions are produced for the articles described in
Table 2. The nodes of the tree contain the
required space of that article version. Zero space means that this
article does not appear on the page at all. Each solution is
represented by a path from root to one of the leaf nodes.
In fact, this scheme also describes a depth-first tree-traversing algorithm. The depth-first search tree produced by the above described ordering of the articles described in Table 2 is shown in Fig. 9.
After defining the best-first generation mechanism for article selections, a method was needed for discarding selections that were known not to produce an acceptable result. The most important restriction was that the material has to fit on the page. Two other restrictions were adopted as well; one stating the minimum allowed area that is occupied by the material on page, and another stating the minimum acceptable priority value for the whole page.
Ordering of the material by area and priority caused the clearly unsuitable solutions to appear neatly within the same branches of the search tree. This meant that when one unsuitable solution was found, it was unnecessary to examine that branch further. An example of cutting a branch due to exceeding the space on a page is shown in Fig. 10. To be exact, since the ordering produced is not strictly best-first but only close to it, some branches with possibly suitable solutions may also be cut. However, considering the reasons behind the best-first ordering, it is enough to produce a sufficiently large amount of possible solutions that pass the test.
Yet another integrity check was used to reject unsuitable combinations. Two articles that were wider than half of the page width, could not fit side to side on the page. Therefore, they should be stacked on top of each other, and thus their summed height should not exceed the page height. After this rule was added to the rejection criteria, the approach actually resembled some more developed bin-packing algorithms, although the problem they are used to solve is different.
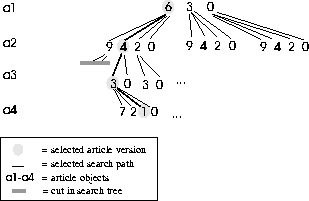
Figure: The previously shown search tree, now with a cut.
The size of the page was defined as 16 units, whereas the lower limit
for the area of the material was set into 14 units.
Formulation of the problem at hand into a form suitable for the application of SA may be approached either by first determining some naturally appealing transitions, or by defining the states first and then determining a group of appropriate transitions. Naturally, the transitions should only lead to states that were defined as part of the state space, and reach all of them. In addition, since at each temperature the system should reach the thermal equilibrium in a reasonable time, it is suggested that there should not be too long minimum paths between pairs of states in the state--transition graph (noted e.g. in Aarts and Korst, 1989). The longer the minimum paths, the longer time (i.e. longer Markov chains) it takes to reach the thermal equilibrium. However, no quantitative advice is given in literature on how to decide what constitutes a "too long minimum path between two states".
The state space should naturally include at least all the states representing acceptable solutions. These are layouts with no articles crossing page borders or overlapping with each other. As these states cannot be characterized before solving the problem, also other kinds of states had to be included in the state space. Practice has also shown that it is useful to have intermediate states representing pseudo-solutions [Aarts and Korst, 1989]. Still, no advice is given on how to extend the state space, i.e.how to decide which conditions of the optimal solution should be relaxed.
It was decided to include extra states by allowing article overlappings during annealing, and thus the objective of no overlappings was coded into the cost funtion. Crossings of page borders, on the other hand, were not allowed even during the annealing. This kind of approach was also suggested by Aarts and Korst (1989), pp. 86--88, for a rather similar problem.
The state transitions were chosen so that an article might at one transition move 1--30 rows within the same column or, alternatively move one column to either direction on the same row, with equal probabilities. Thus there were 32 possible transitions from any state.
Annealing schedule was chosen so that in the initial temperature almost all attempts (over 90%) were accepted. The end temperature was chosen so that less than 10% of the lowest-energy changes were still accepted.
The temperature T was decreased according to the exponential scheme
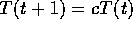, where t and t+1 are consecutive rounds in the
annealing process. The parameter c affecting the speed of annealing
was chosen make the process go from start temperature to the end
temperature in 500 000 rounds. It was possible to calculate these
temperatures beforehand from the types of possible state transitions.
Since in this experiment the article forms, priorities and contents were decided already during selection of the material, only the positions of the articles could contribute to the cost of the page. Avoiding overlaps in the final results was the most important goal to reach for. The total energy of the page therefore consisted of calculating the overlappings:
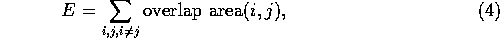
where i and j represent articles on the page. The energy change associated with a transition thus becomes
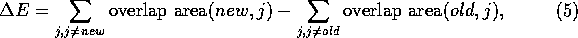
where new is the new article, i.e. the article in the new position, and old respectively the old position before suggested change.
In some cases the optimal solution was visited upon during annealing, but in such a high temperature that the system continues to look for better solutions. As a minor optimization, the best solution found so far was saved and in the end compared with the final solution --- the better of the two was taken as the output of the annealing.
Fig. 11 depicts 20 annealing runs made with one article selection. In many of the runs, a fully acceptable solution (i.e. one with zero overlappings) was found. Many runs also produced results that would not be useful pagination results even with article layout methods.
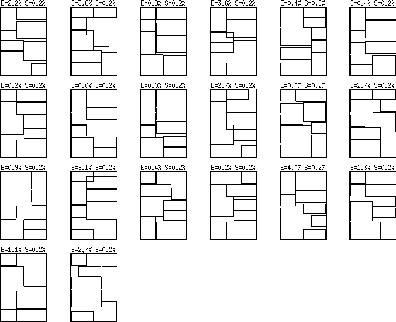
Figure: Annealing results of one article
configuration on 20 rounds. The configurations with only
slight overlap may be considered acceptable, as they may be
adjusted to fit to the page with fine-tuning techniques.
Another test run was made with 18 different article configurations and is shown in Fig. 12. In most cases, a solution with only slight overlap was found, but there were very few results totally without overlap. It should be noted that in many of the examples a completely overlap-free solution may not even exist, despite the attempts to minimize this possibility during article selection.
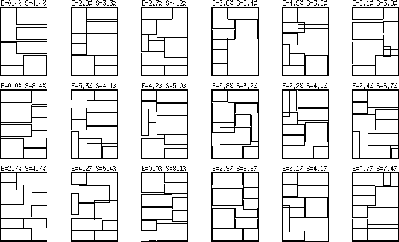
Figure: Annealing results for 18 different article
configurations. Each article selection was produced with the
variable-base adder mechanism. Annealing was then applied to the
selection. E is the amount of overlap, which was used as the energy of
the page. S is the percentage of the extra space on the page that
would be there if the annealing of this selection was perfect. The
total value of the page is S + E.
It is worth noting that slight overlaps in the final result are acceptable if fine-tuning methods (such as described by Kukkonen, 1992) are available for final adjustments. With these methods small overlappings as well as small empty spaces may be deleted by re-arranging the preliminary article layouts. In both Fig. 12 and Fig. 11 the layouts with less than 2% of overlap seem rather acceptable, and as this small difference amounts to about one text line of overlap, it may be taken care of by other means. Thus, from the results with article selection in Fig. 11, it can be seen that 6 out of 20 runs produced an acceptable solution.
Although this method is not a good choice for exactly this problem, some useful components and insights were definitely gained. In retrospect, if selection of article forms is carried out independently of forming the layout, pure bin-packing methods may perform better than simulated annealing. At least it is obvious that some mutually overlapping work was now carried out by the selection and the layout creation processes, since already in the selection it was noticed that articles wider than half the page could not fit side by side. However, it was not obvious how to code this understanding to SA without changing the annealing into something else or disturbing its own internal mechanisms too much.
The problem of the approach may be crystallized as follows: reaching thermal equilibrium takes too long a time, i.e. the probability distribution spreads slowly in terms of steps taken. The three factors affecting the propagation of the probability distribution are the size and connectivity properties of the state space, and the energy jumps between states.
It seems that the major problem with the state space formulation used
in SA1 was that individual state transitions were too local
compared to the size of the state space. It would have been better
either to allow longer jumps on one move, so that the probability of
going over an energy hill would have been higher. It might have been
wise to allow moving an article from side to side, or even exchanging
two articles instead of moving just one. The same effect would have
been achieved by discretizing the state space further.
Admittedly, the previous tentative analysis of the dynamics of the state space is rather intuitive, and an exact mathemathical formulation and analysis as well as practical tests would be required to confirm the analysis.